4.7 Horizontal Alignment

It is necessary to establish the proper relation between design speed and curvature when designing roadway alignment. The two basic elements of horizontal curves are:
  • Curve radius; and
  • Superelevation rate.

4.7.1 General Considerations

There are several general considerations important for safe, smooth flowing, and aesthetically pleasing facilities. These practices, as outlined below, are particularly applicable to
high-speed facilities.
  • Flatter than minimum curvature for any particular design speed should be used where possible, while retaining the minimum guidelines for the most critical conditions.
  • Alignment consistency should be sought. Sharp curves should not follow long tangents or a series of flat curves.
  • Sharp curves should be avoided on long, high fills. It is difficult for drivers to perceive the extent of curvature and adjust their operation accordingly when the adjacent topography does not extend above the level of the roadway.
  • Compound curves (two adjacent curves in the same direction with different radii) should be used with caution and should be avoided on mainlanes where conditions permit the use of simple curves. Where compound curves are used, the ratio of the flatter radius to the sharper radius should not exceed 3:2 (i.e., R
    1
     should not exceed 1.5R
    2
    ). For intersections or other turning roadways (such as loops, connections, and ramps), this ratio may be increased to 2:1 (i.e., R
    1
     may be increased to 2R
    2
    ).
  • Reverse curves (two adjacent curves in opposite directions) on high-speed facilities should include a tangent section of sufficient length to provide adequate superelevation transition between the curves.
  • Broken-back curves (two curves in the same direction with a short tangent between the curves) should be avoided except where very unusual topographical or ROW conditions make other alternatives impractical. This configuration is unexpected by drivers, not pleasing in appearance, and more difficult for freight truck maneuverability.
    It is recommended to provide a minimum tangent length that is at least 15 times the design speed.
     A design exception is not required if this recommended tangent length is not met.
  • Horizontal alignment and its associated design speed should be consistent with other design features and topography. Combination of horizontal and vertical alignments is discussed in
    Section 4.9
    .

4.7.2 Curve Radius

The design of roadway curves should be based on an appropriate relationship between design speed and curvature as well as their joint relationships with superelevation rate and side friction. The minimum radii of curves are important control values in designing for safe operation. Design guidance for low-speed rural town, suburban, urban, and urban core facilities (45-mph and below) is shown in
Table 4-4
. Design guidance for curvature of highspeed (50-mph and above) or rural context facilities is shown in
Table 4-5
,
Table 4-6
and
Table 4-7
for maximum superelevation (e
max
) rates equal to 4 percent, 6 percent, and 8 percent respectively.
For high-speed design conditions, the maximum allowable deflection angle without a horizontal curve is 30 minutes.
For low-speed design conditions, the maximum allowable deflection angle without a horizontal curve is 1 degree.

4.7.3 Superelevation Rate

As a vehicle traverses a horizontal curve, it undergoes a centripetal acceleration that acts toward the center of the curve. Vehicle weight, roadway superelevation, and side friction between the tires and pavement surface sustain this acceleration. The equation that governs vehicle operation on a horizontal curve is:
e + f=V215R
Where:
e =
 superelevation rate, ft/ft
f =
 side friction factor
V =
 vehicle speed, mph
R =
 curve radius, ft
There are practical upper limits to the rate of superelevation.
The Department normally uses a maximum superelevation rate of 6 percent.
 However, a maximum rate of 8 percent may be used where higher superelevation rates or sharper curves are desired. The recommended maximum for facilities where there is a regular occurrence of very-slow moving vehicles, whose operation might be affected by high superelevation rates is 6 percent.
Use of 8 percent should be coordinated with the District Design Engineer prior to implementation and documented in the project files.
To provide designers flexibility in high-speed urban and suburban settings, a maximum superelevation rate of 4 percent may be used instead of a 6 percent or 8 percent superelevation rate.
Freeway facilities are excluded from using a maximum superelevation rate of 4 percent.
4.7.3.1 Methods of Calculating Superelevation Rate
When calculating superelevation on rural and high-speed suburban, urban, and urban core facilities, AASHTO uses a process known as
Method 5
. Method 5 is intended to accommodate overdriving that is likely to occur on flat to intermediate curves. Overdriving on such curves involves little risk that a driver will lose control of the vehicle because superelevation sustains nearly all the lateral acceleration at the average running speed and a large amount of side friction is available for greater speeds. Due to the additional side friction available, Method 5 is used on rural and high-speed suburban, urban, and urban core facilities to provide greater driver comfort and safety.
Where superelevation will be applied to low-speed roads on low-speed rural town, suburban, urban, and urban core facilities, AASHTO uses
Method 2
 superelevation distribution. Method 2 only introduces superelevation after the maximum side friction has been used. Therefore, no superelevation is needed on flatter curves. This method is used on low-speed rural town, suburban, urban, and urban core facilities where, because of various constraints, superelevation frequently cannot be provided. Method 2 ensures driver safety but does not offer the added driver comfort that Method 5 provides.
Table 4-3
provides a summary of scenarios for the use of Method 2 and Method 5. The following assumptions are included in the application of
Table 4-3
.
  • Urban context
     includes Urban Core, Urban, Suburban, and Rural Town.
  • Rural context
     is exclusive of urbanized contexts;
  • Intermediate Speed
     is a range of speeds from 50 – 60 mph that technically falls within what would typically be categorized as a High-speed facility, the Intermediate values are provided in
    Table 4-3
    to give the designer additional flexibility in these transitional areas;
  • The general continuum for the amount of calculated side force on a vehicle in a horizontal curve from greatest to least is as follows:
    • Method 2;
    • Method 5 (4 percent e
      max
      );
    • Method 5 (6 percent e
      max
      ); and
    • Method 5 (8 percent e
      max
      ).
    The designer has the option of selecting a superelevation methodology that either increases the radius and/or decreases the side force for driver comfort on the various facility types listed
    Table 4-3
    ; and
  • Side force should never exceed AASHTO maximums for a given design speed, regardless of the method used.

4.7.4 Superelevation Rates on Low-Speed Rural Town, Suburban, Urban and Urban Core Facilities

Although superelevation is advantageous for traffic operations, various factors often combine to make its use impractical in many rural town, suburban, urban, and urban core areas. These factors include the following:
  • Wide pavement areas;
  • Surface drainage considerations;
  • Frequency of cross streets and driveways; and
  • Need to meet the grade of adjacent property.
For these reasons, horizontal curves on low-speed rural town, suburban, urban, and urban core facilities are frequently designed with normal crown. The centripetal acceleration, in this case, is counteracted solely with side friction. The term
“normal crown”
 (NC) represents an equal downward pavement cross-slope, typically 2 percent, on each side of the axis of rotation.
Low-speed rural town, suburban, urban, and urban core facilities should be designed using NC, such that superelevation is not necessary where practical. This is accomplished by using the negative e-values from
Table 4-4
.
However, when superelevation is needed, a maximum superelevation rate of 4 percent should be used. This is accomplished by using the positive e-values from
Table 4-4
.
Table 4-3: Superelevation Methodology Summary
1
Low-Speed
(≤ 45 mph)
Intermediate-Speed
(50 – 60 mph)
High-Speed
(65 mph and greater)
Urban
All Functional Classifications
(Excluding Freeway Mainlanes,
Ramps and Direct Connectors)
Method 2
Table 4-4
Method 5
4%, 6% or 8% emax
Table 4-5, Table 4-6 or Table 4-7
Method 5
6% or 8% emax
Table 4-6 or Table 4-7
Rural
All Functional Classifications
Method 5
6% or 8% emax
Table 4-6, or Table 4-7
Urban or Rural
Freeway Mainlanes, Ramps, and
Direct Connectors
Method 5
6% or 8% emax
Table 4-6 or Table 4-7
Urban
Frontage Roads
Method 2
Table 4-4
Method 5
4%, 6% or 8% emax
Table 4-5, Table 4-6 or Table 4-7
Method 5
6% or 8% emax
Table 4-6 or Table 4-7
Rural Frontage Roads
Method 5
6% or 8% emax
Table 4 6 or Table 4 7
Urban Ramps for Grade
Separations on Non-Access
Controlled Facilities
Method 2
Table 4 4
Method 5
4%, 6% or 8% emax
Table 4-5, Table 4-6 or Table 4-7
Method 5
6% or 8% emax
Table 4-6 or Table 4-7
Rural Ramps for Grade
Separations on Non-Access
Controlled Facilities
Method 5
6% or 8% emax
Table 4 6 or Table 4 7
Roundabouts and Alternative
Intersections
(Including Approaches)
2
Method 2
Table 4-4
Method 5
4%, 6% or 8% emax
Table 4-5, Table 4-6 or Table 4-7
N/A
Temporary Traffic Control
3
Method 2 expanded
Table 23-1
Low-Volume Off-System Bridges
(approach roadway)
Meet or improve conditions that are typical on the remainder of the roadway
Notes:
  1. The designer has the option of selecting a superelevation methodology that either increases the radius and or decreases the side force for driver comfort on the various facility types listed in this table.
  2. The desired target speed approaching and through roundabouts and other alternative intersection forms should be lower to ensure the proper functioning of the alternative intersection and the resultant safety benefits.
  3. For areas in the TCP phasing of construction that represent what will be left in place for the final permanent condition, the respective permanent condition superelevation method should be utilized.
Table 4-4: Superelevation Rates on Low-speed Rural Town, Suburban, Urban and Urban Core Facilities (Method 2)
Design Speed
e
(%)
15
mph
R (ft)
20
mph
R (ft)
25
mph
R (ft)
30
mph
R (ft)
35
mph
R (ft)
40
mph
R (ft)
45
mph
R (ft)
-4.0
2
54
116
219
375
583
889
1227
-3.0
2
52
111
208
353
544
821
1125
-2.8
2
51
110
206
349
537
808
1107
-2.6
2
51
109
204
345
530
796
1089
-2.5
2,3
51
109
203
343
527
790
1080
-2.4
2
51
108
202
341
524
784
1071
-2.2
2
50
108
200
337
517
773
1055
-2.0
50
107
198
333
510
762
1039
-1.5
4,5
49
105
194
324
495
736
1000
-1.0
4,5
48
103
189
316
480
711
964
-0.5
4,5
48
101
185
308
467
688
931
0
5,6
47
99
181
300
454
667
900
0.5
5
46
97
177
293
441
646
871
1.0
5
45
95
174
286
430
627
844
1.5
5
45
94
170
279
419
610
818
2.0
44
92
167
273
408
593
794
2.2
44
91
165
270
404
586
785
2.4
44
91
164
268
400
580
776
2.6
43
90
163
265
396
573
767
2.8
43
89
161
263
393
567
758
3.0
43
89
160
261
389
561
750
3.2
43
88
159
259
385
556
742
3.4
42
88
158
256
382
550
734
3.6
42
87
157
254
378
544
726
3.8
42
87
155
252
375
539
718
4.0
42
86
154
250
371
533
711
Notes:
  1. Computed using Superelevation Distribution Method 2. See AASHTO’s A Policy on Geometric Design of Highways and Streets for the different types of Superelevation Distribution Methods.
  2. Normal crown values beyond -2.0% should be used for surfaces such as gravel, crushed stone, and earth.
  3. Areas with paved surfaces that receive more frequent rainfall events with high intensities and greater depths than other areas may use 2.5% normal crown.
  4. For the purpose of evaluating existing conditions, normal crown values up to -1.5% may be used
  5. Values ranging from -1.5% to +1.5% should only be used in special circumstances such as intersections
  6. 0% is provided for information purposes only and should not be used for design.
Table 4-4
, which is based on the Method 2 superelevation distribution, shows the relationship of radius, superelevation rate, and design speed for low-speed rural town, suburban, urban, and urban core facility design and should be used to evaluate existing conditions or the need for superelevation for proposed conditions on low-speed rural town, suburban, urban, and urban core facilities.
This table may also be used for design of detour alignments in constrained conditions.
For a normal crown section, the negative e-value (the slope on the outside of the curve) will always be the controlling value for a given design speed.
Example: Given a design speed of 35 mph and a 400-ft radius curve,
Table 4-4
indicates an approximate superelevation rate of 2.4 percent should be used.

4.7.5 Superelevation Rate on Rural and High-Speed Suburban, Urban, and Urban Core Facilities

Table 4-5
,
Table 4-6
and
Table 4-7
show superelevation rates (maximum 4 percent, 6 percent and 8 percent, respectively) for various design speeds and radii based on
Method 5
 superelevation distribution.
These tables should be used for rural and highspeed suburban, urban, and urban core facilities.
For multi-lane facilities, particularly where wide medians are used, the radius applies to the inside edge of the innermost travel lane.
Table 4-5: Minimum Radii and Superelevation Rates
1
 for High-Speed Suburban and Urban Non-Freeway Facilties, e
max
 = 4%
1, 2
 (Method 5)
Design Speed
e
(%)
15
mph
R(ft)
20
mph
R(ft)
25
mph
R(ft)
30
mph
R(ft)
35
mph
R(ft)
40
mph
R(ft)
45
mph
R(ft)
50
mph
R(ft)
55
mph
R(ft)
60
mph
R(ft)
NC
3,5
(Method 2)
7,220
8,650
10,300
RC
4,5
4,940
5,950
7,080
2.2
4,280
5,180
6,190
2.4
3,690
4,500
5,410
2.6
3,130
3,870
4,700
2.8
2,660
3,310
4,060
3.0
2,290
2,860
3,530
3.2
1,980
2,490
3,090
3.4
1,720
2,170
2,700
3.6
1,480
1,880
2,350
3.8
1,260
1,600
2,010
4.0
926
1,190
1,500
Notes:
  1. Computed using Superelevation Distribution Method 5. See AASHTO’s A Policy on Geometric Design of Highways and Streets for the different types of Superelevation Distribution Methods.
  2. Use of e
    max
    =4% should be limited to high-speed urban and suburban areas. Freeway facilities are excluded from using e
    max
    =4%.
  3. a) The term “NC” (normal crown) represents an equal downward cross-slope, typically 2%, on each side of the axis of rotation.
    b) The minimum curve radii for normal crown are suitable up to 3.0%.
    c) 3.0% normal crown should only be used when 3 or more lanes are sloped in the same direction.
    d) 1.5% or flatter normal crown should only be used for the design of special circumstance, such as table-topping intersections, or the evaluation of existing conditions.
  4. . The term “RC” (reverse crown) represents a curve where the downward, or adverse, cross-slope should be removed by superelevating the entire roadway at the normal cross-slope rate.
  5. For curve radii falling between normal crown and reverse crown, rather than interpolation a superelevation rate equal to the normal crown should typically be used
Table 4-6: Minimum Radii and Superelevation Rates
1
 for Rural and High-Speed Suburban, Urban and-Urban Core Facilities, e
max
 = 6%
Design Speed
e
(%)
15
mph
R (ft)
20
mph
R (ft)
25
mph
R (ft)
30
mph
R (ft)
35
mph
R (ft)
40
mph
R (ft)
45
mph
R (ft)
50
mph
R (ft)
55
mph
R (ft)
60
mph
R (ft)
65
mph
R (ft)
70
mph
R (ft)
75
mph
R (ft)
80
mph
R (ft)
NC
2,4
868
1,580
2,290
3,130
4,100
5,230
6,480
7,870
9,410
11,100
12,600
14,100
15,700
17,400
RC
3,4
614
1,120
1,630
2,240
2,950
3,770
4,680
5,700
6,820
8,060
9,130
10,300
11,500
12,900
2.2
543
991
1,450
2,000
2,630
3,370
4,190
5,100
6,110
7,230
8,200
9,240
10,400
11,600
2.4
482
884
1,300
1,790
2,360
3,030
3,770
4,600
5,520
6,540
7,430
8,380
9,420
10,600
2.6
430
791
1,170
1,610
2,130
2,740
3,420
4,170
5,020
5,950
6,770
7,660
8,620
9,670
2.8
384
709
1,050
1,460
1,930
2,490
3,110
3,800
4,580
5,440
6,200
7,030
7,930
8,910
3.0
341
635
944
1,320
1,760
2,270
2,840
3,480
4,200
4,990
5,710
6,490
7,330
8,260
3.2
300
566
850
1,200
1,600
2,080
2,600
3,200
3,860
4,600
5,280
6,010
6,810
7,680
3.4
256
498
761
1,080
1,460
1,900
2,390
2,940
3,560
4,250
4,890
5,580
6,340
7,180
3.6
209
422
673
972
1,320
1,740
2,190
2,710
3,290
3,940
4,540
5,210
5,930
6,720
3.8
176
358
583
864
1,190
1,590
2,010
2,490
3,040
3,650
4,230
4,860
5,560
6,320
4.0
151
309
511
766
1,070
1,440
1,840
2,300
2,810
3,390
3,950
4,550
5,220
5,950
4.2
131
270
452
684
960
1,310
1,680
2,110
2,590
3,140
3,680
4,270
4,910
5,620
4.4
116
238
402
615
868
1,190
1,540
1,940
2,400
2,920
3,440
4,010
4,630
5,320
4.6
102
212
360
555
788
1,090
1,410
1,780
2,210
2,710
3,220
3,770
4,380
5,040
4.8
91
189
324
502
718
995
1,300
1,640
2,050
2,510
3,000
3,550
4,140
4,790
5.0
82
169
292
456
654
911
1,190
1,510
1,890
2,330
2,800
3,330
3,910
4,550
5.2
73
152
264
413
595
833
1,090
1,390
1,750
2,160
2,610
3,120
3,690
4,320
5.4
65
136
237
373
540
759
995
1,280
1,610
1,990
2,420
2,910
3,460
4,090
5.6
58
121
212
335
487
687
903
1,160
1,470
1,830
2,230
2,700
3,230
3,840
5.8
51
106
186
296
431
611
806
1,040
1,320
1,650
2,020
2,460
2,970
3,560
6.0
39
81
144
231
340
485
643
833
1,060
1,330
1,660
2,040
2,500
3,050
Notes:
  1. Computed using Superelevation Distribution Method 5. See AASHTO’s A Policy on Geometric Design of Highways and Streets for the different types of Superelevation Distribution Methods.
  2. a) The term “NC” (normal crown) represents an equal downward cross-slope, typically 2%, on each side of the axis of rotation.
    b) The minimum curve radii for normal crown are suitable up to 3.0%.
    c) 3.0% normal crown should only be used when 3 or more lanes are sloped in the same direction.
    d) 1.5% or flatter normal crown should only be used for the design of special circumstance, such as table-topping intersections, or the evaluation of existing conditions
  3. The term “RC” (reverse crown) represents a curve where the downward, or adverse, cross-slope should be removed by superelevating the entire roadway at the normal cross-slope rate
  4. . For curve radii falling between normal crown and reverse crown, rather than interpolation a superelevation rate equal to the normal crown should typically be used.
  5. Low-Speed values are shown for use on Rural Facilities with low operating speeds. These values are also provided for design exception documentation on High-Speed facilities.
Table 4-7: Minimum Radii and Superelevation Rates
1
 for Rural and High-Speed Suburban, Urban and Urban Core Facilities, e
max
 = 8%
Design Speed
e
(%)
15
mph
R (ft)
20
mph
R (ft)
25
mph
R (ft)
30
mph
R (ft)
35
mph
R (ft)
40
mph
R (ft)
45
mph
R (ft)
50
mph
R (ft)
55
mph
R (ft)
60
mph
R (ft)
65
mph
R (ft)
70
mph
R (ft)
75
mph
R (ft)
80
mph
R (ft)
NC
2,4
932
1,640
2,370
3,240
4,260
5,410
6,710
8,150
9,720
11,500
12,900
14,500
16,100
17,800
RC
3,4
676
1,190
1,720
2,370
3,120
3,970
4,930
5,990
7,150
8,440
9,510
10,700
12,000
13,300
2.2
605
1,070
1,550
2,130
2,800
3,570
4,440
5,400
6,450
7,620
8,600
9,660
10,800
12,000
2.4
546
959
1,400
1,930
2,540
3,240
4,030
4,910
5,870
6,930
7,830
8,810
9,850
11,000
2.6
496
872
1,280
1,760
2,320
2,960
3,690
4,490
5,370
6,350
7,180
8,090
9,050
10,100
2.8
453
796
1,170
1,610
2,130
2,720
3,390
4,130
4,950
5,850
6,630
7,470
8,370
9,340
3.0
415
730
1,070
1,480
1,960
2,510
3,130
3,820
4,580
5,420
6,140
6,930
7,780
8,700
3.2
382
672
985
1,370
1,820
2,330
2,900
3,550
4,250
5,040
5,720
6,460
7,260
8,130
3.4
352
620
911
1,270
1,690
2,170
2,700
3,300
3,970
4,700
5,350
6,050
6,800
7,620
3.6
324
572
845
1,180
1,570
2,020
2,520
3,090
3,710
4,400
5,010
5,680
6,400
7,180
3.8
300
530
784
1,100
1,470
1,890
2,360
2,890
3,480
4,140
4,710
5,350
6,030
6,780
4.0
277
490
729
1,030
1,370
1,770
2,220
2,720
3,270
3,890
4,450
5,050
5,710
6,420
4.2
255
453
678
955
1,280
1,660
2,080
2,560
3,080
3,670
4,200
4,780
5,410
6,090
4.4
235
418
630
893
1,200
1,560
1,960
2,410
2,910
3,470
3,980
4,540
5,140
5,800
4.6
215
384
585
834
1,130
1,470
1,850
2,280
2,750
3,290
3,770
4,310
4,890
5,530
4.8
193
349
542
779
1,060
1,390
1,750
2,160
2,610
3,120
3,590
4,100
4,670
5,280
5.0
172
314
499
727
991
1,310
1,650
2,040
2,470
2,960
3,410
3,910
4,460
5,050
5.2
154
284
457
676
929
1,230
1,560
1,930
2,350
2,820
3,250
3,740
4,260
4,840
5.4
139
258
420
627
870
1,160
1,480
1,830
2,230
2,680
3,110
3,570
4,090
4,640
5.6
126
236
387
582
813
1,090
1,390
1,740
2,120
2,550
2,970
3,420
3,920
4,460
5.8
115
216
358
542
761
1,030
1,320
1,650
2,010
2,430
2,840
3,280
3,760
4,290
6.0
105
199
332
506
713
965
1,250
1,560
1,920
2,320
2,710
3,150
3,620
4,140
6.2
97
184
308
472
669
909
1,180
1,480
1,820
2,210
2,600
3,020
3,480
3,990
6.4
89
170
287
442
628
857
1,110
1,400
1,730
2,110
2,490
2,910
3,360
3,850
6.6
82
157
267
413
590
808
1,050
1,330
1,650
2,010
2,380
2,790
3,240
3,720
6.8
76
146
248
386
553
761
990
1,260
1,560
1,910
2,280
2,690
3,120
3,600
7.0
70
135
231
360
518
716
933
1,190
1,480
1,820
2,180
2,580
3,010
3,480
7.2
64
125
214
336
485
672
878
1,120
1,400
1,720
2,070
2,470
2,900
3,370
7.4
59
115
198
312
451
628
822
1,060
1,320
1,630
1,970
2,350
2,780
3,250
7.6
54
105
182
287
417
583
765
980
1,230
1,530
1,850
2,230
2,650
3,120
7.8
48
94
164
261
380
533
701
901
1,140
1,410
1,720
2,090
2,500
2,970
8.0
38
76
134
214
314
444
587
758
960
1200
1,480
1,810
2,210
2,670
Notes:
  1. . Computed using Superelevation Distribution Method 5. See AASHTO’s A Policy on Geometric Design of Highways and Streets for the different types of Superelevation Distribution Methods.
  2. a) The term “NC” (normal crown) represents an equal downward cross-slope, typically 2%, on each side of the axis of rotation.
    b) The minimum curve radii for normal crown are suitable up to 3.0%.
    c) 3.0% normal crown should only be used when 3 or more lanes are sloped in the same direction.
    d) 1.5% or flatter normal crown should only be used for the design of special circumstance, such as table-topping intersections, or the evaluation of existing conditions
  3. The term “RC” (reverse crown) represents a curve where the downward, or adverse, cross-slope should be removed by super elevating the entire roadway at the normal cross-slope rate.
  4. For curve radii falling between normal crown and reverse crown, rather than interpolation a superelevation rate equal to the normal crown should typically be used.

4.7.6 Superelevation Transition Length

Superelevation transition is the general term denoting the change in cross slope from a normal crown section to the full superelevated section or vice versa. To meet the requirements of comfort and safety, the superelevation transition should occur over a length adequate for the usual travel speeds.
Transition lengths should also account for potential future traveled way widening, including widening associated with the ultimate typical section in a schematic.
Preferable design values for length of superelevation transition are based on a given maximum relative gradient between profiles of the edge of traveled way and the axis of rotation.
Table 4-8
shows recommended maximum relative gradient values. Transition length on this basis is directly proportional to the total superelevation, which is the product of the lane width and the change in cross slope.
Table 4-8: Maximum Relative Gradient (G) for Superelevation Transition
Design Speed
(mph)
Maximum
Relative Gradient
1
(%)
Equivalent Maximum
Relative Slope (run:rise)
15
0.89
1:112
20
0.80
1:125
25
0.73
1:137
30
0.67
1:150
35
0.62
1:162
40
0.57
1:175
45
0.53
1:187
≥50
0.50
1:200
Notes:
  1. Maximum relative gradient for profile between edge of traveled way and axis of rotation.
Preferable transition length, L
CT
, can be calculated using the following equation:
LCT(preferable)=CSWG
Where:
L
CT (preferable)
 =
Calculated preferable transition length, ft
CS =
 Change in cross slope of superelevated pavement, percent
W =
 distance between the axis of rotation and the edge of traveled way, ft
G =
 maximum relative gradient (%).
Example determinations of superelevation transition are shown in
Figure 4-2
.
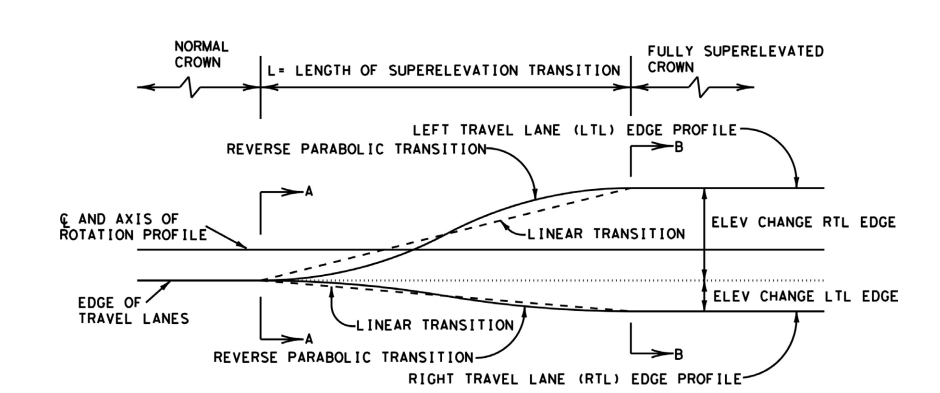
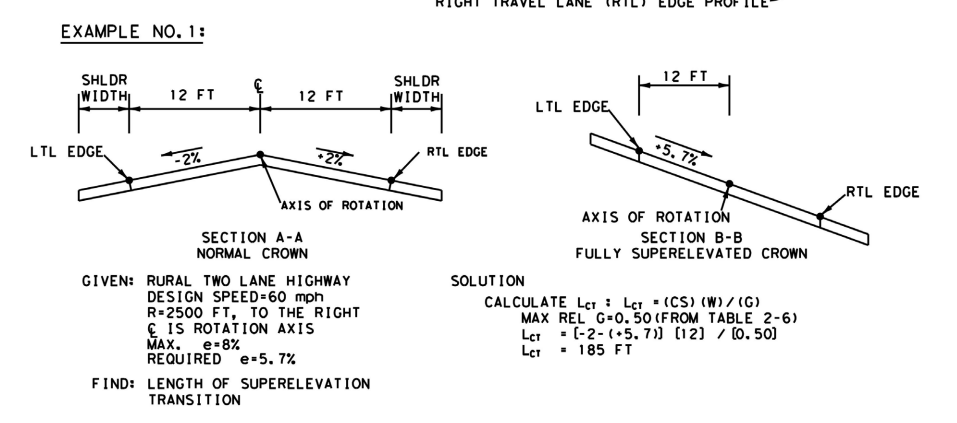
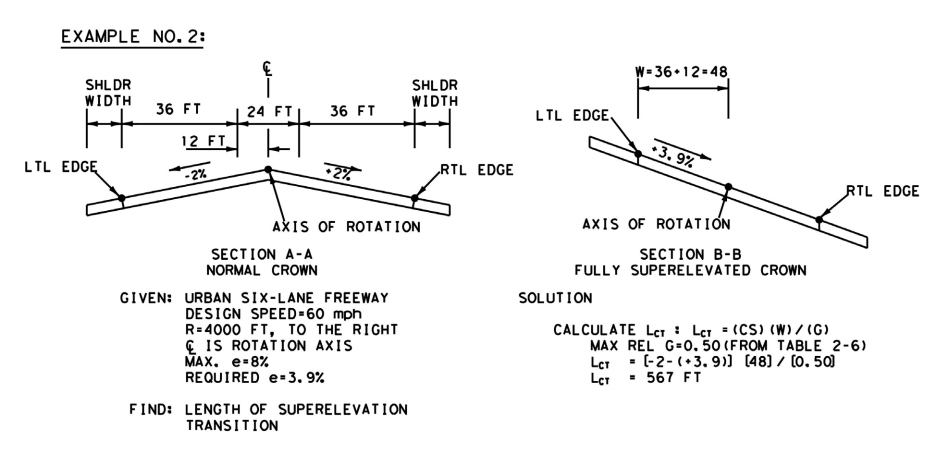
Determination of Length of Superelevation Transition ( click in image to see full-size image)Determination of Length of Superelevation Transition Example no. 1( click in image to see full-size image)Determination of Length of Superelevation Transition Example no. 2 ( click in image to see full-size image)
Figure 4-2: Determination of Length of Superelevation Transition
As the number of lanes to be transitioned increases, the length of superelevation transition increases proportionately with the increased width. While strict adherence to the length (L
CT
) calculation is preferable, the length for multilane facilities may become impractical for design purposes (e.g., drainage problems, avoiding bridges, accommodating merge/diverge condition).
A minimum length (L
CT
), can be calculated using adjustment factors as shown in
Table 4-9
, such that the transition length formula becomes:
LCT(min)=CSWGb
where “b” is defined in Table 4-9.
In the case of one lane being rotated, “b” is 1.0, such that L
CT (min)
 = L
CT (preferable)
Table 4-9: Multilane Adjustment Factor
1
Number of Lanes Rotated
(n)
Adjustment Factor
2
(b)
1.5
0.83
2
0.75
2.5
0.70
3
0.67
3.5
0.64
4
0.63
4.5
0.61
5
0.60
Notes:
  1. . These adjustment factors are directly applicable to undivided facilities. For divided facilities where the axis of rotation is not the edge of traveled way, see AASHTO’s A Policy on Geometric Design of Highways and Streets.
  2. For all values of n, b = 1+0.5(n−1) / n (Calculations are rounded to the nearest hundredth)

4.7.7 Superelevation Transition Placement

The transition with respect to the termini of a simple (circular) curve should be placed to minimize lateral acceleration and the vehicle's lateral motion. The recommended allocation of superelevation transition on the tangent, preceding or following a curve, is provided on
Table 4-10
. For superelevation on bridge structures, it is preferred to begin/end superelevation at the bridge bent line. When spiral curves are present on an existing facility and alignment modifications aren’t practical, refer to
AASHTO’s A Policy on Geometric Design of Highways and Streets
for transition distribution.
Table 4-10: Portion of Superelevation Transition Located on the Tangent
1
Design Speed (mph)
No. of Lanes Rotated
1.0
1.5
2.0 - 2.5
3.0 - 3.5
15 - 45
0.80
0.85
0.90
0.90
50 - 80
0.70
0.75
0.80
0.85
Notes:
  1. These values are recommendations based on prevailing research. A value between 0.7 and 0.9 for all speeds and rotated widths is considered acceptable. Refer to AASHTO’s A Policy on Geometric Design of Highways and Streets for additional information.
Care must be exercised in designing the length and location of the superelevation transition. Pavement surfaces should be modeled to ensure proper drainage, especially near the high or low portions of Type I or III vertical curves (see
Figure 4-5
for curve types).
A plot of roadway contours may assist with the verification of grades and identification of drainage problems in areas of superelevation transition. Preferably,
a minimum profile grade line (PGL) of 0.5 percent and minimum edge-of-pavement (EOP) profile grade of 0.2 percent (0.5 percent for curbed roadways) should be maintained throughout the
superelevation transition section
.
 At a minimum, either criterion should be met.
On existing alignments, whenever reverse curves are closely spaced and superelevation transition lengths overlap, transition lengths (L
CT
) should be adjusted to ensure that roadway cross slopes are in the proper direction for each horizontal curve. For proposed construction of new facilities, the tangent section between reverse curves should be of sufficient length such that minimum transition lengths for each transition do not overlap.

4.7.8 Superelevation Transition Type

Linear or reverse parabolic transitions may be used for attaining superelevation.
Where appearance is a factor (e.g., curbed sections and retaining walls) use of reverse parabolic is recommended.
 This produces an outer edge profile that is smooth, undistorted, and pleasing in appearance. However,
for bridges, linear transitions are generally preferred
 for constructability, ride quality, and lower cost.
Notate the transition type in the plans to ensure the transition is properly constructed.
Figure 4-2
shows reverse parabolic and linear transitions over the full length of the transition. Refer to
AASHTO's A Policy on Geometric Design of Highways and Streets
for alternative methods for developing smooth-edge profiles over the length of the transition.

4.7.9 Sight Distance on Horizontal Curves

Where an object off the pavement restricts sight distance, such as a bridge pier, bridge railing, median barrier, retaining wall, building, cut slope or natural growth,
the minimum radius of curvature is determined by the stopping sight distance.
The following equation applies only to circular curves longer than the stopping sight distance (S<L) for the pertinent design speed. For example, with a 50-mph design speed and a curve with a 1,150-ft radius, a clear sight area with a horizontal sight line offset (HSO) of approximately 20-ft is needed for stopping sight distance.
HSO=R1-cos28.65SR
Where:
HSO =
 horizontal sight line offset, ft
S =
 stopping sight distance (
Table 4-23
), ft
R =
 radius at centerline of inner most travel lane, ft
This method for calculating HSO is only exact when both the vehicle and sight obstruction are located within the horizontal curve. When the vehicle or sight obstruction are located outside of the horizontal curve (i.e., S>L) this method will result in an HSO slightly larger than required. In many instances the resulting additional clearance will not be significant. In some cases, the design should be checked either by using graphical procedures (2D or 3D) or computational methods to verify HSO. NHCRP 910 provides computational methods for verifying HSO.
In cases where complex geometries or discontinuous objects cause sight obstructions, graphical methods may be useful in determining available sight distance and associated offset requirements. Graphical methods may also be used when the circular curve is shorter than the stopping sight distance.
To check horizontal sight distance on the inside of a curve graphically, sight lines equal to the required sight distance on horizontal curves should be reviewed to ensure that obstructions such as buildings, hedges, barrier railing, and high ground do not restrict the sight distance required in either direction.
Figure 4-3
illustrates a graphical approach to determining horizontal sight distance in a curve.
Where sufficient stopping sight distance is not available because a railing, longitudinal barrier or other features constitutes a sight obstruction, alternative designs should be considered. Potential alternatives include:
  • Increasing the offset to the obstruction; or
  • Increasing the radius.
However, the alternative should not incorporate a shoulder width on the inside of the curve more than 12-ft because of the concern that drivers will use wider shoulders as a passing or travel lane.
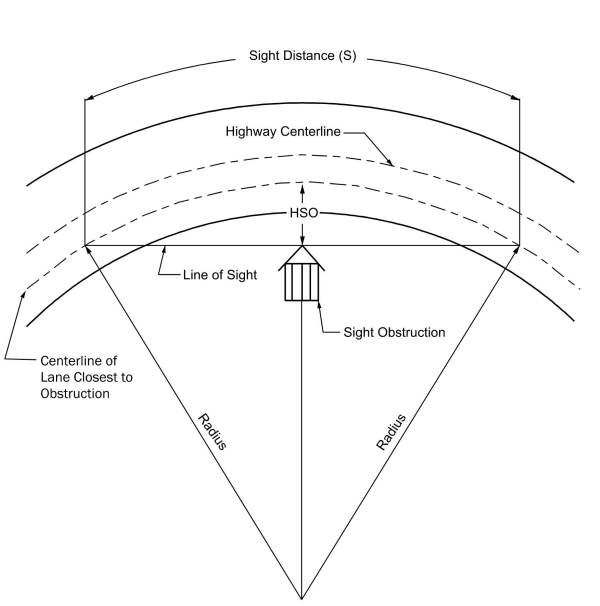
Diagram Illustrating Components for Determining Horizontal Sight Distance ( click in image to see full-size image)
Figure 4-3: Diagram Illustrating Components for Determining Horizontal Sight Distance
Source: AASHTO A Policy on Geometric Design of Highways and Streets