4.11.5 Sight Distance at Under-Crossings
Sight distance through a grade crossing should be at least the minimum stopping sight distance, or longer. Line of sight may be obstructed by an overpass structure and can limit the sight distance for the operator. Where practical, provide the minimum length of sag vertical curve at grade separated structures. Where economically feasible, for two-lane roadways, the passing sight distance should be maintained.
When the minimum sag vertical curve length based on headlight sight distance, as described in
, is achieved for vertical clearances of 14-ft or higher, then
and subsequent equations are not applicable. However, if any of the following conditions occur, then the under-crossing curve length as shown in
and subsequent equations should be verified based on the applicable stopping sight distance (SSD):
- The minimum sag vertical curve length based on SSD for headlights is not met;
- The comfort control (lighting) criteria is used to establish the sag vertical curve length; and
- The vertical clearance is less than 14-ft.
The general equations for sag vertical curve length at under-crossings are:
Case 1 –
Sight distance greater than length of vertical Curve (S>L):Where:
L =
length of vertical curve, ft S =
sight distance, ft C =
vertical clearance, ft h
eye height, ft 1
=h
height of object, ft 2
=A =
algebraic difference in grades, percent Case 2 –
Sight distance less than length of vertical curve (S<L)Using an eye height of 8.0-ft for a truck driver and an object height of 2.0-ft for the taillights of a vehicle, the following equations can be derived:
Case 1 –
Sight distance greater than length of vertical curve (S>L):Case 2 –
Sight distance less than length of vertical curve (S<L)Where:
L =
length of vertical curve, ft S =
sight distance, ft C =
vertical clearance, ft h
height of eye, ft 1
=h
height of object, ft 2
=A =
algebraic difference in grades, percent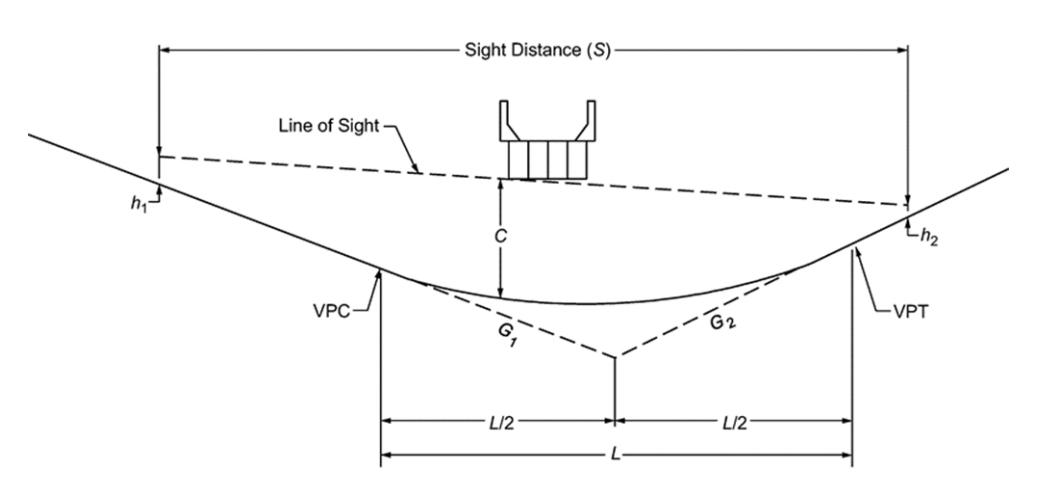
Figure 4-29: Sight Distance at Under-Crossings
Source: AASHTO A Policy on Geometric Design of Highways and Streets