Sequent Depth

A direct solution for sequent depth, d
s
 is possible for free surface flow in a rectangular conduit on a flat slope using Equation 8-23. If the slope is greater than about 10 percent, a more complex solution is required to account for the weight component of the water. FHWA
Hydraulic Engineering Circular 14
provides more detail for such conditions.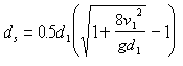
EquationObject255290
Equation 8-23.
where:
  • d
    s
    = sequent depth, ft. or m
  • d
    1
    = depth of flow (supercritical), ft. or m
  • v
    1
    = velocity of flow at depth d, ft./s or m/s.
A direct solution for sequent depth in a circular conduit is not feasible. However, an iterative solution is possible by following these equations:
  • Select a trial sequent depth, d
    s
    , and apply Equation 8-24 until the calculated discharge is equal to the design discharge. Equation 8-24 is reasonable for slopes up to about 10 percent.
  • Calculate the first moments of area for the supercritical depth of flow, d
    1
    , and sequent depth, d
    s
    , using Equation 8-25.
  • This equation uses the angle β shown in Figure 8‑16, which you calculate by using Equation 8-26.
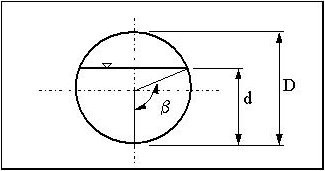    Determination of Angle b (click in image to see full-size image)
    Figure 8-16. Determination of Angle b
    CAUTION: Some calculators and spreadsheets may give only the principal angle for β in Equation 8-26 (i.e., -π/2 radians ≤ β ≤ π/2 radians).
  • Use Equation 8-27 to calculate the areas of flow for the supercritical depth of flow and sequent depth.
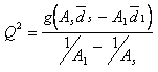  • EquationObject256292
    Equation 8-24.
where:
  • Q
     = discharge, cfs or m
    3
    /s
  • A
    s
    = area of flow at sequent depth, sq.ft. or m
    2
  • A
    s
    d
    s
    = first moment of area about surface at sequent depth, cu.ft. or m
    3
  • A
    1
    d
    1
    = first moment of area about surface at supercritical flow depth, cu.ft. or m
    3
    .
EquationObject257293
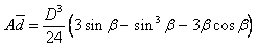
Equation 8-25.
where:
  • Ad
     = first moment of area about water surface, cu.ft. or m
    3
  • D
     = conduit diameter, ft. or m
  • β = angle shown in Figure 8‑16 and calculated using Equation 8-26.
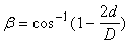
EquationObject258295
Equation 8-26.
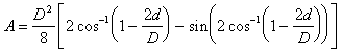
EquationObject259296
Equation 8-27.
Equation 8-24 applies to other conduit shapes having slopes of about 10 percent or less. The first moment of area about the surface, A d_
, is dependent on the shape of the conduit and depth of flow. A relationship between flow depth and first moment of area must be acquired or derived.