Direct Step Backwater Method
The Direct Step Backwater Method uses the same basic equations as the Standard Step Backwater Method but is simpler to use because no iteration is necessary. In the Direct Step Method, an increment (or decrement) of water depth (δd) is chosen and the distance over which the depth change occurs is computed. The accuracy depends on the size of δd. The method is appropriate for prismatic channel sections such as occur in most conduits. It is useful for estimating supercritical profiles and subcritical profiles.
- Choose a starting point and starting water depth (d1). This starting depth depends on whether the profile is supercritical or subcritical. Generally, for culverts, refer to outlet depth and set d1to the value of H0. Otherwise, you may use the following conditions to establish d1:
- For a mild slope (dc< du) and free surface flow at the outlet, begin at the outlet end. Select the higher of critical depth (dc) and tailwater depth (TW). Supercritical flow may occur in a culvert on a mild slope. However, most often, the flow will be subcritical when mild slopes exist. Check this assumption.
- For a steep slope (dc> du), where the tailwater exceeds critical depth but does not submerge the culvert outlet, begin at the outlet with the tailwater as the starting depth.
- For a steep slope in which tailwater depth is lower than critical depth, begin the water surface profile computations at the culvert entrance starting at critical depth and proceed downstream to the culvert exit. This implies inlet control, in which case the computation may be necessary to determine outlet velocity but not headwater.
- For a submerged outlet in which free surface flow begins along the barrel, use the barrel depth, D, as the starting depth. Begin the backwater computations at the location where the hydraulic grade line is coincident with the soffit of the culvert.
- The following steps assume subcritical flow on a mild slope culvert for a given discharge, Q, through a given culvert of length, L, at a slope, So. Calculate the following at the outlet end of the culvert based on the selected starting depth (d1):
- cross-section area of flow, A
- wetted perimeter, WP
- velocity, v, from Equation 8-17
- velocity head, hv, using Equation 8-9
- specific energy, E, using Equation 8-18
- friction slope, Sf, using Equation 8-13.
- Assign the subscript 1 to the above variables (A1, WP1, etc.).
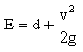 Equation 8-18.where:
Equation 8-18.where:- E= specific energy (ft. or m)
- d= depth of flow (ft. or m)
- v= average velocity of flow (fps or m/s)
- g= gravitational acceleration = 32.2 ft/ s2or 9.81 m/s2.
- Choose an increment or decrement of flow depth, δ d: if d1> du, use a decrement (negative δ d); otherwise, use an increment. The increment, δ d, should be such that the change in adjacent velocities is not more than 10%.
- Calculate the parameters A, WP, v, E, and Sfat the new depth, d2= d1+ δ d, and assign the subscript 2 to these (e.g., A2, WP2, etc.).
- Determine the change in energy, δ E, using Equation 8-19.
- Calculate the arithmetic mean friction slope using Equation 8-20.
- Using Equation 8-21, determine the distance, δ L, over which the change in depth occurs.
- Consider the new depth and location to be the new starting positions (assign the subscript1to those values currently identified with the subscript2) and repeat steps 3 to 7, summing the incremental lengths, δ L, until the total length, Σ L, equals or just exceeds the length of the culvert. You may use the same increment throughout or modify the increment to achieve the desired resolution. Such modifications are necessary when the last total length computed far exceeds the culvert length and when high friction slopes are encountered. If the computed depth reaches the barrel rise (D) before reaching the culvert inlet, skip step 9 and refer to the to complete the analysis.
- The last depth (d2) established is the depth at the inlet (Hi) and the associated velocity is the inlet, vi. Calculate the headwater using Equation 8-15.
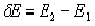 Equation 8-19.
Equation 8-19.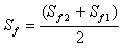 Equation 8-20.
Equation 8-20.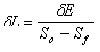 Equation 8-21.
Equation 8-21.