Depth in Conduits
The equations for
apply to conduits, too. Determine critical depth for a rectangular conduit using
and the discharge per barrel. Calculate critical depth for circular and pipe-arch or irregular shapes by trial and error use of
. For a circular conduit, use Equation 6‑17 and Equation 6‑18 to determine the area, A, and top width, T, of flow, respectively. For other shapes, acquire or derive relationships from depth of flow, area, and top width.
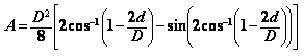
Equation 6-17.
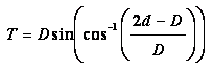
Equation 6-18.
where:
- A= section area of flow, sq. ft. or m2
- T= width of water surface, ft. or m
- d= depth of flow, ft. or m
- D= pipe diameter, ft. or m
- the cos-1 (θ) is the principal value in the range 0 ≤ θ ≤ π.
Use
to determine uniform depth. For most shapes, a direct solution of Equation 6-3 for depth is not possible. The
discussed in Chapter 7 is applicable. For rectangular shapes, area, A, and wetted perimeter, WP are simple functions of flow depth. For circular pipe, compute area using Equation 6-17, and compute wetted perimeter using Equation 6-19. For other shapes, acquire or derive the relationship from depth of flow, area, and wetted perimeter.
Refer to the table below for recommended Manning’s roughness coefficients for conduit.
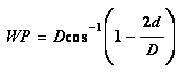
Equation 6-19.