Section 2: Flow in Conduits

Open Channel Flow or Pressure Flow

When a conduit is not submerged, the principles of
open channel flow
apply. When the conduit is submerged, pressure flow exists because the water surface is not open to the atmosphere, and the principles of conduit flow apply. For circular pipes flowing full, Equation 6‑3 becomes:
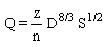
EquationObject210231
Equation 6-16.
where:
  • Q = discharge (cfs or m
    3
    /s)
  • z = 0.4644 for English measurement or 0.3116 for metric.
  • n = Manning’s roughness coefficient
  • D = pipe diameter, ft. or m
  • S = slope of the energy gradeline (ft./ft. or m/m) (For uniform, steady flow, S = channel
  • slope, ft./ft. or m/m).

Depth in Conduits

The equations for
critical depth
apply to conduits, too. Determine critical depth for a rectangular conduit using
Equation 6-12
and the discharge per barrel. Calculate critical depth for circular and pipe-arch or irregular shapes by trial and error use of
Equation 6-13
. For a circular conduit, use Equation 6‑17 and Equation 6‑18 to determine the area, A, and top width, T, of flow, respectively. For other shapes, acquire or derive relationships from depth of flow, area, and top width.
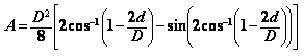
EquationObject211232
Equation 6-17.
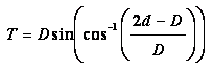
EquationObject212233
Equation 6-18.
where:
  • A
     = section area of flow, sq. ft. or m
    2
  • T
     = width of water surface, ft. or m
  • d
     = depth of flow, ft. or m
  • D
     = pipe diameter, ft. or m
  • the cos-1 (θ) is the principal value in the range 0 ≤ θ ≤ π.
Use
Equation 6-3
to determine uniform depth. For most shapes, a direct solution of Equation 6-3 for depth is not possible. The
Slope Conveyance Procedure
discussed in Chapter 7 is applicable. For rectangular shapes, area, A, and wetted perimeter, WP are simple functions of flow depth. For circular pipe, compute area using Equation 6-17, and compute wetted perimeter using Equation 6-19. For other shapes, acquire or derive the relationship from depth of flow, area, and wetted perimeter.
Refer to the table below for recommended Manning’s roughness coefficients for conduit.
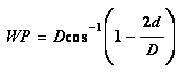
EquationObject213234
Equation 6-19.

Roughness Coefficients

The following table provides roughness coefficients for conduits.
Recommended Culvert Conduit Roughness Coefficients
Type of Conduit
n-Value
Concrete Box
0.012
Concrete Pipe
0.012
Smooth-lined metal pipe
0.012
Smooth lined plastic pipe
0.012
Corrugated metal pipe
0.015-0.027
Structural plate pipe
0.027-0.036
Long span structural plate
0.031
Corrugated metal (paved interior)
0.012
Plastic
0.012-0.024

Energy

The energy equation, Equation 6-6, applies to conduit flow, too. Additionally, the following concepts apply to conduit flow.
  • For pressure flow, the depth, d, represents the distance from the flowline to the hydraulic grade line.
  • For pressure flow, the slope of the energy grade line and hydraulic grade line through the conduit are parallel and are represented by the friction slope.
  • Compute friction losses, h
    f
    , as the product of friction slope and length of conduit.
  • Consider the kinetic energy coefficient (α) equal to unity.
  • Other losses include entrance losses, exit losses, and junction losses.
Refer to
Chapter 8
for directions to accommodate such losses for culvert design and
Chapter 10
for storm drain design.
Compute the velocity head at any location in a conduit using Equation 6-20.
where:
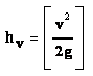
EquationObject214235
Equation 6-20.
where:
  • v
     = flow velocity in culvert (ft./s or m/s).
  • g
     = the gravitational acceleration = 32.2 ft/ s
    2
     or 9.81 m/s
    2
    .
The friction slope represents the slope of the energy grade line and is based upon Manning's Equation, rearranged as follows:
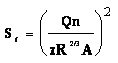
EquationObject215236
Equation 6-21.
where:
  • S
    f
    = friction slope (ft./ft. or m/m)
  • z
    = 1.486 for English measurements and 1.0 for metric.

Steep Slope versus Mild Slope

When critical depth (d
c
) is higher than uniform depth (d
u
), the slope is steep. The conduit may flow completely full (pressure flow) or partly full (free surface flow). The free surface flow may be supercritical or subcritical depending on tailwater conditions.
When critical depth is lower than uniform depth, the slope is termed mild. Pressure flow or free surface flow may occur. Free surface flow is most likely to be subcritical within the conduit.
The shape of the free water surface is dependent on whether the conduit slope is steep or mild and on the tailwater conditions. The
Standard Step Procedure
described in Chapter 7 accommodates the differences in water surface shape.