NRCS Curve Number Loss Model

NRCS
has developed a procedure to divide total depth of rainfall into soil retention, initial abstractions, and effective rainfall. This parameter is referred to as a curve number (CN). The CN is based on soil type, land use, and vegetative cover of the watershed. The maximum possible soil retention is estimated using a parameter that represents the impermeability of the land in a watershed. Theoretically, CN can range from 0 (100% rainfall infiltration) to 100 (impervious). In practice, based on values tabulated in NRCS 1986, the lowest CN the designer will likely encounter is 30, and the maximum CN is 98.
The CN may also be adjusted to account for wet or dry antecedent moisture conditions. Dry soil conditions are referred to as CN I, average conditions (those calculated using Estimating the CN) are referred to as CN II, and wet soils are referred to as CN III. Antecedent moisture conditions should be estimated considering a minimum of a five-day period. Antecedent soil moisture conditions also vary during a storm; heavy rain falling on a dry soil can change the soil moisture condition from dry to average to wet during the storm period.
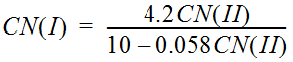
EquationObject150165
Equation 4-34.
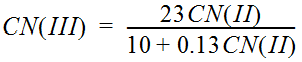
EquationObject151166
Equation 4-35.
Hydrologic Soil Groups
Soil properties influence the relationship between rainfall and runoff by affecting the rate of infiltration. NRCS divides soils into four hydrologic soil groups based on infiltration rates (Groups A-D). Urbanization has an effect on soil groups, as well. See Table 4-17 for more information.
Table 4-17: Hydrologic Soil Groups
Soil group
Description
Soil type
Range of loss rates
(in./hr.)
(mm/hr.)
A
Low runoff potential due to high infiltration rates even when saturated
Deep sand, deep loess, aggregated silts
0.30-0.45
7.6-11.4
B
Moderately low runoff potential due to moderate infiltration rates when saturated
Shallow loess, sandy loam
0.15-0.30
3.8-7.6
C
Moderately high runoff potential due to slow infiltration rates
Soils in which a layer near the surface impedes the downward movement of water or soils with moderately fine to fine texture
Clay loams, shallow sandy loam, soils low in organic content, and soils usually high in clay
0.05-0.15
1.3-3.8
D
High runoff potential due to very slow infiltration rates
Soils that swell significantly when wet, heavy plastic clays, and certain saline soils
0.00-0.05
1.3
Estimating the CN
Rainfall infiltration losses depend primarily on soil characteristics and land use (surface cover). The NRCS method uses a combination of soil conditions and land use to assign runoff CNs. Suggested runoff curve numbers are provided in Table 4-18, Table 4-19, Table 4-20, and Table 4-21. Note that CNs are whole numbers.
For a watershed that has variability in land cover and soil type, a composite CN is calculated and weighted by area.
Table 4-18: Runoff Curve Numbers For Urban Areas
Cover type and hydrologic condition
Average percent impervious area
A
B
C
D
Open space (lawns, parks, golf courses, cemeteries, etc.):
Poor condition (grass cover < 50%)
68
79
86
89
Fair condition (grass cover 50% to 75%)
49
69
79
84
Good condition (grass cover > 75%)
39
61
74
80
Paved parking lots, roofs, driveways, etc. (excluding right-of-way)
98
98
98
98
Streets and roads:
Paved; curbs and storm drains (excluding right-of-way)
98
98
98
98
Paved; open ditches (including right-of-way)
83
89
92
93
Gravel (including right-of-way)
76
85
89
91
Dirt (including right-of-way)
72
82
87
89
Western desert urban areas:
Natural desert landscaping (pervious areas only)
63
77
85
88
Artificial desert landscaping (impervious weed barrier, desert shrub with 1- to 2-in. sand or gravel mulch and basin borders)
96
96
96
96
Urban districts:
Commercial and business
85
89
92
94
95
Industrial
72
81
88
91
93
Residential districts by average lot size:
1/8 acre or less (townhouses)
65
77
85
90
92
1/4 acre
38
61
75
83
87
1/3 acre
30
57
72
81
86
1/2 acre
25
54
70
80
85
1 acre
20
51
68
79
84
2 acres
12
46
65
77
82
Developing urban areas: Newly graded areas (pervious area only, no vegetation)
77
86
91
94
Notes: Values are for average runoff condition, and I
a
 = 0.2S. The average percent impervious area shown was used to develop the composite CNs. Other assumptions are: impervious areas are directly connected to the drainage system, impervious areas have a CN of 98, and pervious areas are considered equivalent to open space in good hydrologic condition.
Table 4-19: Runoff Curve Numbers For Cultivated Agricultural Land
Cover type
Treatment
Hydrologic condition
A
B
C
D
Fallow
Bare soil
-
77
86
91
94
Crop residue cover (CR)
Poor
Good
76
74
85
83
90
88
93
90
Row crops
Straight row (SR)
Poor
Good
72
67
81
78
88
85
91
89
SR + CR
Poor
Good
71
64
80
75
87
82
90
85
Contoured (C)
Poor
Good
70
65
79
75
84
82
88
86
C + CR
Poor
Good
69
64
78
74
83
81
87
85
Contoured & terraced (C&T)
Poor
Good
66
62
74
71
80
78
82
81
C&T + CR
Poor
Good
65
61
73
70
79
77
81
80
Small grain
SR
Poor
Good
65
63
76
75
84
83
88
87
SR + CR
Poor
Good
64
60
75
72
83
80
86
84
C
Poor
Good
63
61
74
73
82
81
85
84
C + CR
Poor
Good
62
60
73
72
81
80
84
83
C&T
Poor
Good
61
59
72
70
79
78
82
81
C&T + CR
Poor
Good
60
58
71
69
78
77
81
80
Close-seeded or broadcast legumes or rotation meadow
SR
Poor
Good
66
58
77
72
85
81
89
85
C
Poor
Good
64
55
75
69
83
78
85
83
C&T
Poor
Good
63
51
73
67
80
76
83
80
Notes: Values are for average runoff condition, and I
a
 = 0.2S. Crop residue cover applies only if residue is on at least 5% of the surface throughout the year. Hydrologic condition is based on a combination of factors affecting infiltration and runoff: density and canopy of vegetative areas, amount of year-round cover, amount of grass or closed-seeded legumes in rotations, percent of residue cover on land surface (good > 20%), and degree of roughness. Poor = Factors impair infiltration and tend to increase runoff. Good = Factors encourage average and better infiltration and tend to decrease runoff.
Table 4-20: Runoff Curve Numbers For Other Agricultural Lands
Cover type
Hydrologic condition
A
B
C
D
Pasture, grassland, or range-continuous forage for grazing
Poor
Fair
Good
68
49
39
79
69
61
86
79
74
89
84
80
Meadow – continuous grass, protected from grazing and generally mowed for hay
-
30
58
71
78
Brush – brush-weed-grass mixture, with brush the major element
Poor
Fair
Good
48
35
30
67
56
48
77
70
65
83
77
73
Woods – grass combination (orchard or tree farm)
Poor
Fair
Good
57
43
32
73
65
58
82
76
72
86
82
79
Woods
Poor
Fair
Good
45
36
30
66
60
55
77
73
70
83
79
77
Farmsteads – buildings, lanes, driveways, and surrounding lots
-
59
74
82
86
Notes: Values are for average runoff condition, and I
a
 = 0.2S. Pasture: Poor is < 50% ground cover or heavily grazed with no mulch, Fair is 50% to 75% ground cover and not heavily grazed, and Good is > 75% ground cover and lightly or only occasionally grazed. Meadow: Poor is < 50% ground cover, Fair is 50% to 75% ground cover, Good is > 75% ground cover. Woods/grass: CNs shown were computed for areas with 50 percent grass (pasture) cover. Other combinations of conditions may be computed from CNs for woods and pasture. Woods: Poor = forest litter, small trees, and brush destroyed by heavy grazing or regular burning. Fair = woods grazed but not burned and with some forest litter covering the soil. Good = woods protected from grazing and with litter and brush adequately covering soil.
Table 4-21: Runoff Curve Numbers For Arid And Semi-arid Rangelands
Cover type
Hydrologic condition
A
B
C
D
Herbaceous—mixture of grass, weeds, and low-growing brush, with brush the minor element
Poor
Fair
Good
80
71
62
87
81
74
93
89
85
Oak-aspen—mountain brush mixture of oak brush, aspen, mountain mahogany, bitter brush, maple, and other brush
Poor
Fair
Good
66
48
30
74
57
41
79
63
48
Pinyon-juniper—pinyon, juniper, or both; grass understory
Poor
Fair
Good
75
58
41
85
73
61
89
80
71
Sagebrush with grass understory
Poor
Fair
Good
67
51
35
80
63
47
85
70
55
Saltbush, greasewood, creosote-bush, blackbrush, bursage, palo verde, mesquite, and cactus
Poor
Fair
Good
63
55
49
77
72
68
85
81
79
88
86
84
Notes: Values are for average runoff condition, and I
a
 = 0.2S. Hydrologic Condition: Poor = < 30% ground cover (litter, grass, and brush overstory), Fair = 30% to 70% ground cover, Good = > 70% ground cover. Curve numbers for Group A have been developed only for desert shrub.
Soil Retention
The potential maximum retention (S) is calculated as:
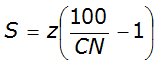
EquationObject152167
Equation 4-36.
Where:
  • z
     = 10 for English measurement units, or 254 for metric
  • CN
     = runoff curve number
Equation 4-36 is valid if S is less than the rainfall excess, defined as precipitation (P) minus runoff (R) or S < (P-R). This equation was developed mainly for small watersheds from recorded storm data that included total rainfall amount in a calendar day but not its distribution with respect to time. Therefore, this method is appropriate for estimating direct runoff from 24-hour or 1-day storm rainfall.
Initial Abstraction
The initial abstraction consists of interception by vegetation, infiltration during early parts of the storm, and surface depression storage.
Generally, I
a
 is estimated as: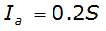
EquationObject153168
Equation 4-37.
Effective Rainfall Runoff Volume
The effective rainfall (or the total rainfall minus the initial abstractions and retention) used for runoff hydrograph computations can be estimated using:
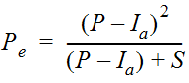
EquationObject154169
Equation 4-38.
Where:
  • P
    e
     = accumulated excess rainfall (in.)
  • I
    a
     = initial abstraction before ponding (in.)
  • P = total depth of rainfall (in.)
  • S = potential maximum depth of water retained in the watershed (in.)
Substituting Equation 4-37, Equation 4-38 becomes:
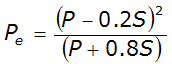
EquationObject155170
Equation 4-39.
P
e
 and P have units of depth, P
e
 and P reflect volumes and are often referred to as volumes because it is usually assumed that the same depths occurred over the entire watershed. Therefore P
e
 is considered the volume of direct runoff per unit area, i.e., the rainfall that is neither retained on the surface nor infiltrated into the soil. P
e
 also can be applied sequentially during a storm to compute incremental precipitation for selected time interval Δt.
Climatic Adjustment of CN
NRCS curve numbers, estimated (predicted) using the procedure described in
Estimating the CN
, may be adjusted to account for the variation of climate within Texas. The adjustment is applied as follows: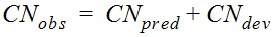
EquationObject156171
Equation 4-40.
Where:
  • CN
    obs
     = CN adjusted for climate
  • CN
    pred
     = Estimated CN from NRCS procedures described in
    Estimating the CN
  • CN
    dev
     = Deviation of CN
    obs
     from CN
    pred
     = climatic adjustment factor
In two studies (Hailey and McGill 1983, Thompson et al. 2003) CN
dev
 was computed for gauged watersheds in Texas as CN
obs
 - CN
pred
 based on historical rainfall and runoff volumes. These studies show that CN
dev
 varies by location within the state.
The following excerpt (Thompson et al. 2003) guides the designer in selection and application of the appropriate climatic adjustment to the predicted CN.
Given the differences between CN
obs
 and CN
pred
, it is possible to construct a general adjustment to CN
pred
 such that an approximation of CN
obs
 can be obtained. The large amount of variation in CN
obs
 does not lend to smooth contours or function fits. There is simply an insufficient amount of information for these types of approaches. However, a general adjustment can be implemented using regions with a general adjustment factor. Such an approach was taken and is presented in Figure 4-20.
The bulk of rainfall and runoff data available for study were measured near the I-35 corridor. Therefore, estimates for this region are the most reliable. The greater the distance from the majority of the watershed that were part of this study, then the more uncertainty must be implied about the results. For the south high plains, that area south of the Balcones escarpment, and the coastal plain, there was insufficient data to make any general conclusions.
Application of the tool is straightforward. For areas where adjustment factors are defined (see Figure 4-20) the analyst should:
  • Determine CN
    pred
     using the normal NRCS procedure.
  • Find the location of the watershed on the design aid (Figure 4-21). Determine an adjustment factor from the design aid and adjust the curve number.
  • Examine Figure 4-21 and find the location of the watershed. Use the location of the watershed to determine nearby study watersheds. Then refer to Figure 4-20 and Table 4-22, Table 4-23, Table 4-24, Table 4-25, and Table 4-26 and determine CN
    pred
     and CN
    obs
     for study watersheds near the site in question, if any are near the watershed in question.
  • Compare the adjusted curve number with local values of CN
    obs
    .
The result should be a range of values that are reasonable for the particular site.
As a comparison, the adjusted curve number from Hailey and McGill (Figure 4-22) can be used.
A lower bound equivalent to the curve number for AMC I (dry antecedent conditions), or a curve number of 60, whichever is greater, should be considered.
Note that CN values are whole numbers. Rounding of values of CN
pred
 in the tables may be required.
Judgment is required for application of any hydrologic tool. The adjustments presented on Figure 4-20 are no exception. A lower limit of AMC I may be used to prevent an overadjustment downward. For areas that have few study watersheds, the Hailey and McGill approach should provide some guidance on the amount of reduction to CN
pred
 is appropriate, if any.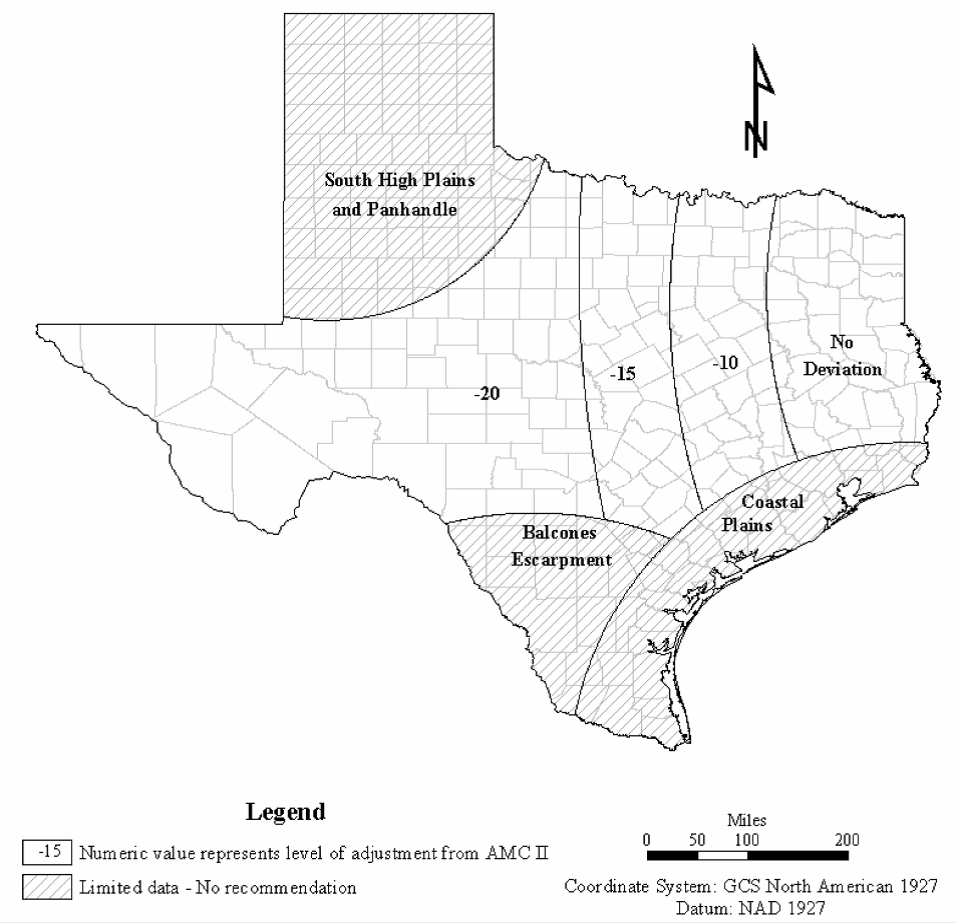
Climatic adjustment factor CNdev (click in image to see full-size image)
Figure 4-20. Climatic adjustment factor CN
dev
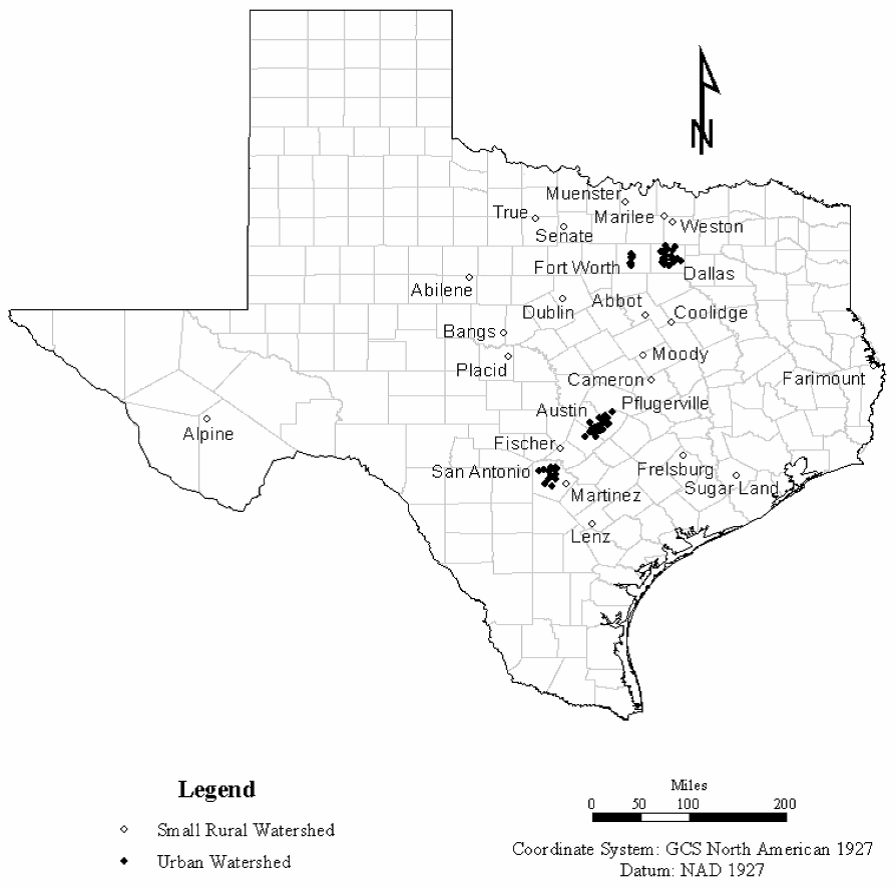
Location of CNdev watersheds (click in image to see full-size image)
Figure 4-21. Location of CNdev watersheds
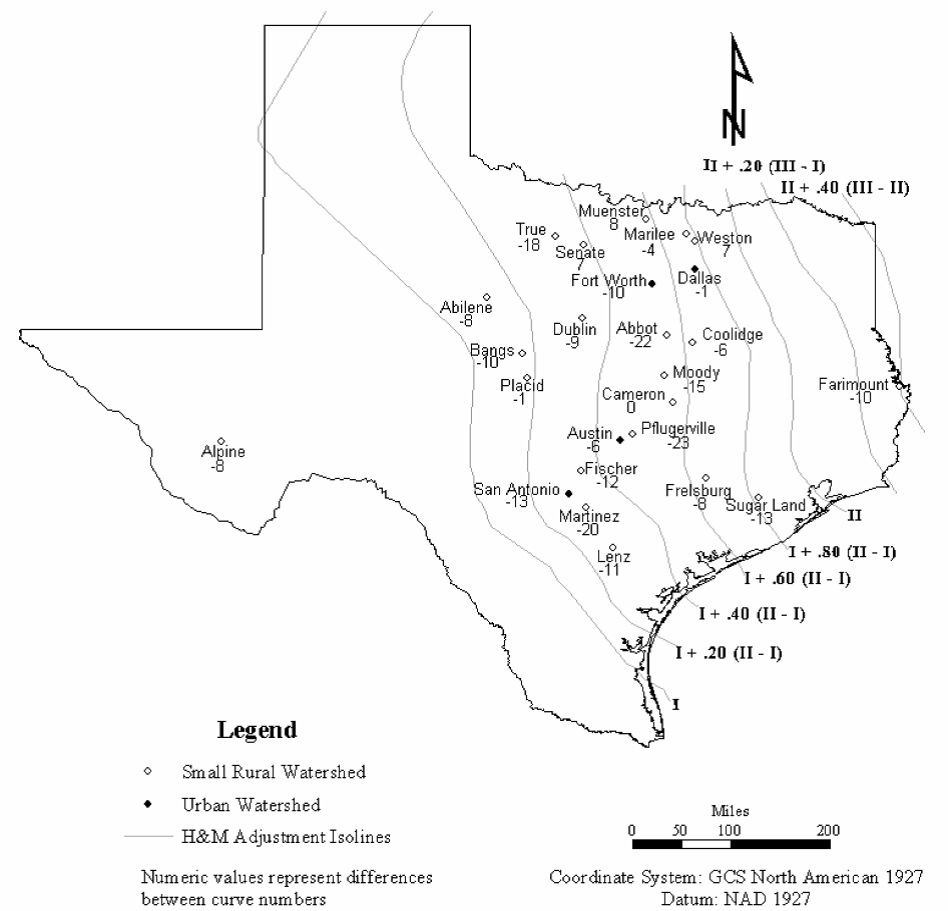
Climatic adjustment of CN - comparison of Hailey and McGill adjusted curve numbers, CNH&M, with CNobs. Negative differences indicate that CNH&M is larger than CNobs. Also shown are the lines of equal adjustment to curve number from Hailey and McGill’s (1983)
Climatic adjustment of CN - comparison of Hailey and McGill adjusted curve numbers, CNH&M, with CNobs. Negative differences indicate that CNH&M is larger than CNobs. Also shown are the lines of equal adjustment to curve number from Hailey and McGill’s (1983) Figure 4. (click in image to see full-size image)
Table 4-22: CN
obs
, CN
pred
, and CN
dev
 for the Austin region
USGS Gauge ID
Quad Sheet Name
CN
obs
CN
pred
CN
dev
8154700
Austin West
59
68.9
-9.9
8155200
Bee Cave
65
70.7
-5.7
8155300
Oak Hill
64
69.8
-5.8
8155550
Austin West
50
87.3
-37.3
8156650
Austin East
60
83.6
-23.6
8156700
Austin East
78
86.6
-8.6
8156750
Austin East
66
86.8
-20.8
8156800
Austin East
66
87
-21
8157000
Austin East
68
88.3
-20.3
8157500
Austin East
67
89.1
-22.1
8158050
Austin East
71
83.9
-12.9
8158100
Pflugerville West
60
72.6
-12.6
8158200
Austin East
62
75.6
-13.6
8158400
Austin East
79
88.9
-9.9
8158500
Austin East
71
85.6
-14.6
8158600
Austin East
73
76.7
-3.7
8158700
Driftwood
69
74.5
-5.5
8158800
Buda
64
73.3
-9.3
8158810
Signal Hill
64
69.8
-5.8
8158820
Oak Hill
60
67.9
-7.9
8158825
Oak Hill
49
67.2
-18.2
8158840
Signal Hill
74
69.8
4.2
8158860
Oak Hill
60
68
-8
8158880
Oak Hill
67
79.4
-12.4
8158920
Oak Hill
71
77.5
-6.5
8158930
Oak Hill
56
75.2
-19.2
8158970
Montopolis
56
77.7
-21.7
8159150
Pflugerville East
63
78.8
-15.8
Table 4-23: CN
obs
, CN
pred
, and CN
dev
 for the Dallas Region
USGS Gauge ID
Quad Sheet Name
CN
obs
CN
pred
CN
dev
8055580
Garland
85
85.2
-0.2
8055600
Dallas
82
86.1
-4.1
8055700
Dallas
73
85.5
-12.5
8056500
Dallas
85
85.8
-0.8
8057020
Dallas
75
85.5
-10.5
8057050
Oak Cliff
75
85.7
-10.7
8057120
Addison
77
80.2
-3.2
8057130
Addison
89
82.9
6.1
8057140
Addison
78
86.8
-8.8
8057160
Addison
80
90.3
-10.3
8057320
White Rock Lake
85
85.7
-0.7
8057415
Hutchins
73
87.8
-14.8
8057418
Oak Cliff
85
79.1
5.9
8057420
Oak Cliff
80
81
-1
8057425
Oak Cliff
90
82.9
7.1
8057435
Oak Cliff
82
81.1
0.9
8057440
Hutchins
67
79.1
-12.1
8057445
Hutchins
60
86.5
-26.5
8061620
Garland
82
85
-3
8061920
Mesquite
85
86
-1
8061950
Seagoville
82
85.3
-3.3
Table 4-24: CN
obs
, CN
pred
, and CN
dev
 for the Fort Worth Region
Gauge ID
Quad Sheet Name
CN
obs
CN
pred
CN
dev
8048520
Fort Worth
72
82.3
-10.3
8048530
Fort Worth
69
86.7
-17.7
8048540
Covington
73
88
-15
8048550
Haltom City
74
91.2
-17.2
8048600
Haltom City
65
84.3
-19.3
8048820
Haltom City
67
83.4
-16.4
8048850
Haltom City
72
83
-11
Table 4-25: CN
obs
, CN
pred
, and CN
dev
 for the San Antonio Region
USGS Gauge ID
Quad Sheet Name
CN
obs
CN
pred
CN
dev
8177600
Castle Hills
70
84.8
-14.8
8178300
San Antonio West
72
85.7
-13.7
8178555
Southton
75
84.2
-9.2
8178600
Camp Bullis
60
79.7
-19.7
8178640
Longhorn
56
78.4
-22.4
8178645
Longhorn
59
78.2
-19.2
8178690
Longhorn
78
84.4
-6.4
8178736
San Antonio East
74
92.3
-18.3
8181000
Helotes
50
79.2
-29.2
8181400
Helotes
56
79.8
-23.8
8181450
San Antonio West
60
87.3
-27.3
Table 4-26: CN
obs
, CN
pred
, and CN
dev
 for the Small Rural Watersheds
USGS Gauge ID
Quadrangle Sheet Name
CN
obs
CN
pred
CN
dev
8025307
Fairmount
53
55.4
-2.4
8083420
Abilene East
65
84.7
-19.7
8088100
True
60
85.9
-25.9
8093400
Abbott
61
88.1
-27.1
8116400
Sugarland
70
82.9
-12.9
8159150
Pflugerville East
55
83.7
-28.7
8160800
Freisburg
56
67.8
-11.8
8167600
Fischer
51
74.3
-23.3
8436520
Alpine South
64
86.4
-22.4
8435660
Alpine South
48
86.7
-38.7
8098300
Rosebud
88
80.5
7.5
8108200
Yarrelton
77
79.9
-2.9
8096800
Bruceville
62
80
-18
8094000
Bunyan
60
78.4
-18.4
8136900
Bangs West
51
75.8
-24.8
8137000
Bangs West
52
74.5
-22.5
8137500
Trickham
53
76.5
-23.5
8139000
Placid
53
74.6
-21.6
8140000
Mercury
63
74.4
-11.4
8182400
Martinez
52
80
-28
8187000
Lenz
53
83.8
-30.8
8187900
Kenedy
63
73.3
-10.3
8050200
Freemound
80
79.6
0.4
8057500
Weston
80
78.2
1.8
8058000
Weston
86
80.1
5.9
8052630
Marilee
80
85.4
-5.4
8052700
Aubrey
74
84.1
-10.1
8042650
Senate
59
63.4
-4.4
8042700
Lynn Creek
50
62.5
-12.5
8042700
Senate
56
62
-6
8042700
Senate
65
55.9
9.1
8063200
Coolidge
70
79.4
-9.4