Kinematic Wave Overland Flow Model

A kinematic wave model is a conceptual model of watershed response that uses laws of conservation of mass and momentum to simulate overland and channelized flows. The model represents the watershed as a wide open channel, with inflow equal to the excess precipitation. Then it simulates unsteady channel flow over the surface to compute the watershed runoff hydrograph. The watershed is represented as a set of overland flow planes and collector channels.
In kinematic wave modeling, the watershed shown in Figure 4-27(a) is represented in Figure 4-27(b) as series of overland flow planes (gray areas) and a collector channel (dashed line). The collector channel conveys flow to the watershed outlet.
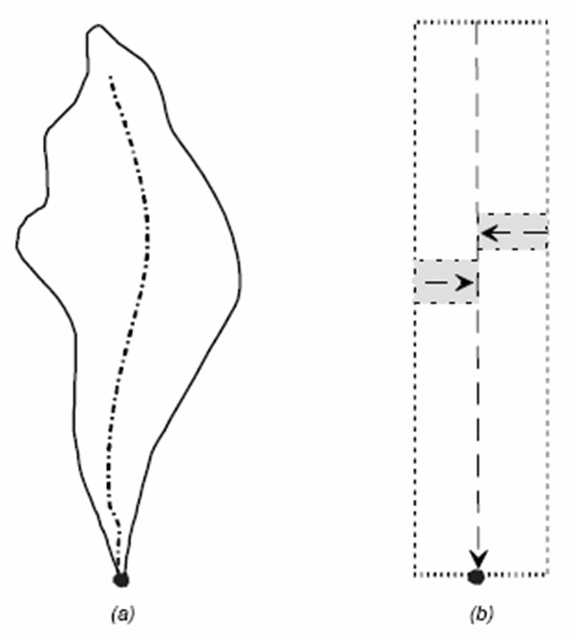
Kinematic wave model representation of a watershed (USACE 2000) (click in image to see full-size image)
Figure 4-27. Kinematic wave model representation of a watershed (USACE 2000)
The equations used to define conservation of mass and momentum are the Saint Venant equations. The conservation of mass equation is:
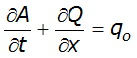
EquationObject173190
Equation 4-57.
Where:
  • A
     = cross sectional area of flow (ft
    2
    , m
    2
    )
  • T
     = time (sec.)
  • Q
     = flow rate (cfs, m
    3
    /sec.)
  • x
     = distance along the flow path (ft, m)
  • q
    o
     = lateral discharge added to the flow path per unit length of the flow path (cfs/ft, m
    3
    /sec./m)
The momentum equation energy gradient is approximated by:
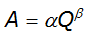
EquationObject174191
Equation 4-58.
Where:
  • a and b
     = coefficients related to the physical properties of the watershed.
Substituting Equation 4-56 into Equation 4-55 yields a single partial differential equation in Q:
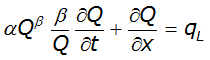
EquationObject175192
Equation 4-59.
Where:
  • q
    L
     = lateral inflow (cfs/ft, m
    3
    /s/m)
Equation 4-54 can be expressed in terms of Manning’s n, wetted perimeter, and bed slope by substituting the following expression for
α𝑄
β
 into Equation 4-56:
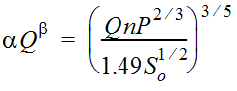
EquationObject176194
Equation 4-60.
Where:
  • n
     = Manning’s roughness coefficient
  • P
     = wetted perimeter (ft, m)
  • S
    o
     = flow plane slope (ft/ft, m/m)
The solution to the resulting equation, its terms, and basic concepts are detailed in Chow (1959) and other texts.