Hydrograph Routing

In some cases, the watershed of interest will be divided into subbasins. This is necessary when ground conditions vary significantly between subbasin areas, or when the total watershed area is sufficiently large that variations in precipitation depth within the watershed must be modeled. A rainfall-runoff method (unit hydrograph or kinematic wave) will produce a flow hydrograph at the outlet of each subbasin. Before these hydrographs can be summed to represent flow at the watershed outlet, the effects of travel time and channel/floodplain storage between the subbasin outlets and watershed outlet must be accounted for. The process of starting with a hydrograph at a location and recomputing the hydrograph at a downstream location is called hydrograph routing.
Figure 4-28 shows an example of a hydrograph at upstream location A, and the routed hydrograph at downstream location B. The resulting delay in flood peak is the travel time of the flood hydrograph. The resulting decrease in magnitude of the flood peak is the attenuation of the flood hydrograph.
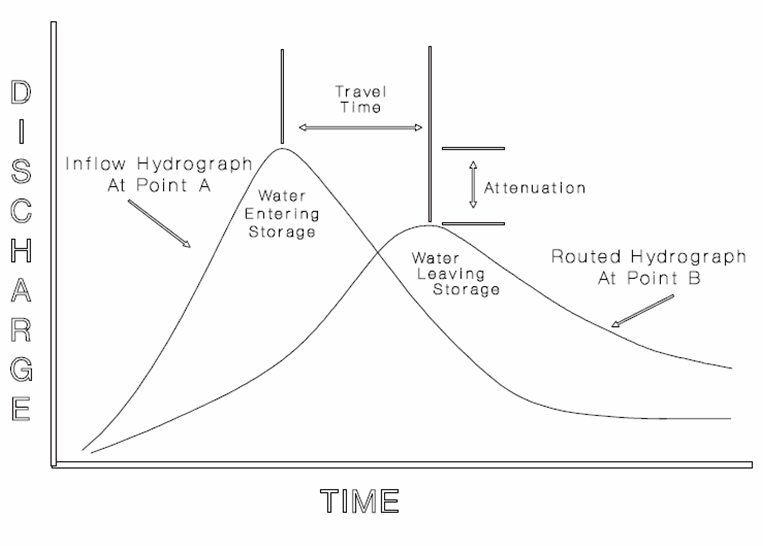
Hydrograph routing (USACE 1994) (click in image to see full-size image)
Figure 4-28. Hydrograph routing (USACE 1994)
There are two general methods for routing hydrographs: hydrologic and hydraulic. The methods are distinguished by which equations are solved to compute the routed hydrograph.
Hydrologic methods solve the equation of continuity (conservation of mass), and typically rely on a second relationship (such as relation of storage to outflow) to complete the solution. The equation of continuity can be written as:
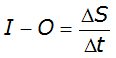
EquationObject177195
Equation 4-61.
Where:
  • I
     = average inflow to reach or storage area during Dt
  • O
     = average outflow to reach or storage area during Dt
  • S
     = storage in reach or storage area
  • Dt
     = time step
Hydrologic methods are generally most appropriate for steep slope conditions with no significant backwater effects. Hydrologic routing methods include (USACE 1994):
  • Modified Puls—for a single reservoir or channel modeled as series of level-pool reservoirs.
  • Muskingum—channel modeled as a series of sloped-pool reservoirs.
  • Muskingum-Cunge—enhanced version of Muskingum method incorporating channel geometry and roughness information.
Most hydrologic software applications capable of multi-basin analysis offer a selection of hydrologic routing methods.
Hydraulic routing methods solve the Saint Venant equations. These are the one-dimensional equations of continuity (Equation 4-60) and conservation of momentum (Equation 4-61) written for open-channel flow. The equations are valid for gradually varied unsteady flow.
The one-dimensional equation of continuity is:
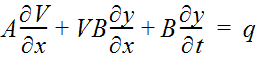
EquationObject178196
Equation 4-62.
Where:
  • A
    = cross-sectional flow area
  • V
     = average velocity of water
  • x
     = distance along channel
  • B
     = water surface width
  • y
     = depth of water
  • t
     = time
  • q
     = lateral inflow per unit length of channel
The one-dimensional equation of conservation of momentum is:
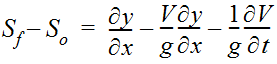
EquationObject179197
Equation 4-63.
Where:
  • S
    f
     = friction slope
  • S
    o
     = channel bed slope
  • g
     = acceleration due to gravity
Hydraulic routing methods are computationally more intensive than hydrologic methods and are distinguished by which terms in the momentum equation (Equation 4-61) are included (not neglected) in the solution algorithm. Hydraulic routing methods include (USACE 1994):
  • Dynamic wave (all terms of St. Venant equations)
  • Diffusion wave
  • Kinematic wave
One-dimensional unsteady open-channel flow software applications implicitly route hydrographs from one location to another by solving for depth and velocity at all locations (cross sections) in a stream reach (or network of reaches) for every time step. The hydraulic routing method employed is defined by the solution algorithm of the software application. Some applications allow the user to select which hydraulic routing method is used, while other applications support only one method.
The most robust routing method (in terms of steep/mild stream slope and with/without backwater effects) is dynamic wave routing.
Selection of Routing Method
Selection of an appropriate routing method depends on several factors. The application of any method will be improved if observed data are available for calibration/verification of routing parameters. Generally, hydrologic methods are most suitable for steeper reaches having little or no backwater effects resulting from high stages downstream of the routing reach. Hydraulic methods are generally more appropriate for a wider range of channel slopes, including gradual slopes, and can accommodate backwater effects. The exception to this is the Muskingum-Cunge method, which does not perform well with steep-rising hydrographs in gradual slopes, or backwater conditions. Of all methods, only the dynamic wave routing method is appropriate for steep and gradual slopes, as well as with or without backwater conditions.
As a baseline approach, the designer may consider using the Muskingum-Cunge method in cases having steep slope (greater than 10 feet per mile) and no backwater effects. This method, which is described in Chow (1988) and Fread (1993), has the advantage that it will incorporate the shape of the cross section into computations. In some cases, cross section data may be obtained from existing hydraulic models of the reach. If channel geometry data are unavailable, then the Muskingum or modified Puls methods, which are described below, may be used. However, these two methods should be avoided for channel routing applications unless observed data are available for calibration/verification of routing parameters.
In cases having backwater that significantly affect the storage-outflow relationship of the routing reach, and thereby significantly affect the routed hydrograph, the dynamic wave, diffusion wave, and modified Puls methods are appropriate.
All methods, except for kinematic wave, are appropriate in cases having a channel slope between 2 to 10 feet per mile, no backwater effects, and satisfying the condition given by Equation 4-62 (USACE 1994):
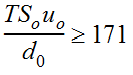
EquationObject180198
Equation 4-64.
Where:
  • T
     = hydrograph duration (s)
  • S
    o
     = average friction or slope (ft/ft)
  • u
    o
     = mean velocity (ft/s)
  • d
    o
     = average flow depth (ft)
Only the dynamic wave, diffusion wave, and Muskingum-Cunge methods are appropriate in cases having a channel slope less than 2 feet per mile, no backwater effects, and satisfying the condition given by Equation 4-63 (USACE 1994):
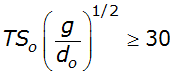
EquationObject181199
Equation 4-65.
Where:
  • g
     = 32.2 ft/s
In cases having a channel slope less than 2 feet per mile, no backwater effects, and not satisfying the condition given by Equation 4-63, then only the dynamic wave method is appropriate.
It may be tempting for the designer to select the dynamic wave routing method as a general approach for all conditions. However, the designer will find that the substantial amount of information (detailed and closely-spaced cross section geometry data) required to construct a one-dimensional unsteady flow model, and the significant time required to ensure that the model is running properly without numerical instabilities, will provide motivation to identify a suitable hydrologic routing method when appropriate. If hydrologic methods are not appropriate for the case under consideration, then an unsteady flow model may be required to properly route flows.