Statistical Rationale
The results of numerous and extensive “before-and-after” studies substantiates the general propriety and value of the 85th percentile criterion.
Statistical techniques show that a normal probability distribution will occur when a random sample of traffic is measured. From the resulting frequency distribution curves, one finds that a certain percentage of drivers drive too fast for the existing conditions and a certain percentage of drivers travel at an unreasonably slow speed compared to the trend of traffic.
Most cumulative speed distribution curves “break” at approximately 15 percent and 85 percent of the total number of observations (see Figure 3-1). Consequently, the motorists observed in the lower 15 percent are considered to be traveling unreasonably slow and those observed above the 85th percentile value are assumed to be exceeding a safe and reasonable speed. Because of the steep slope of the distribution curve below the 85th percentile value, it can readily be seen that posting a speed below the critical value would penalize a large percentage of reasonable drivers.
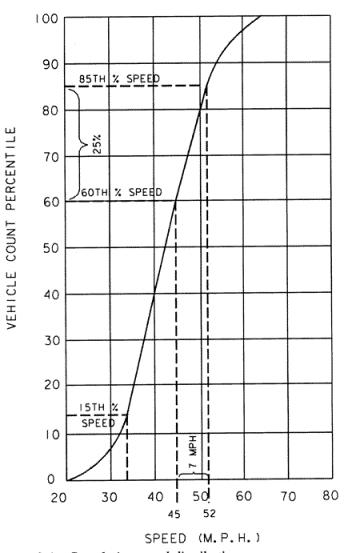
Figure 3-1. Cumulative speed distribution curve
The example illustrated in Figure 3-1 shows that a speed posted for 7 miles per hour below the 85th percentile speed would unfairly penalize 25 percent of the drivers who would otherwise be considered to be driving at a reasonable and prudent speed. Therefore, for purposes of speed zoning, the maximum posted speed should be as near as possible to the 85th percentile value, and whenever minimum speed zones are used, the minimum posted speed should be within 5 miles per hour of the 15th percentile value. (See Chapter 2, Section 2, for additional information on
. )
Experience proves these findings valid and shows that the 85th percentile speed is the one characteristic of traffic speeds that most closely conforms to a speed limit which is considered safe and reasonable.