Pressure Flow Method

By definition, pressure flow methods represent high flow conditions. Figure 9-13 shows a high flow condition in which the water surface at the upstream face of the bridge has impinged the lowchord but the downstream face is not submerged. You may approximate this condition as a sluice gate using Equation 9-7. You need to assume successive elevations at cross section 3 (y
3
) until the calculated discharge in Equation 9-7 is equal to the design discharge within a reasonable tolerance.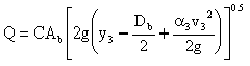
EquationObject270324
Equation 9-7.
where:
  • Q
     = calculated discharge (cfs or m
    3
    /s)
  • C
     = discharge coefficient (0.5 suggested)
  • A
    b
    = net area under bridge (sq. ft. or m
    2
    )
  • y
    3
    = depth of flow at cross section 3 (ft. or m)
  • D
    b
    = height of lowchord from mean stream bed elevation (ft. or m).
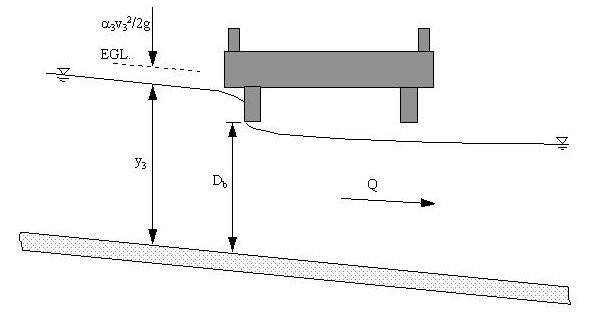
Sluice Gate Type Pressure Flow (click in image to see full-size image)
Figure 9-13. Sluice Gate Type Pressure Flow
Figure 9-14 shows a submerged bridge opening with a tailwater lower than the overtopping elevation Equation 9-8 represents orifice flow. You need to assume successive elevations at cross section 3 (y
3
) until the calculated discharge in Equation 9-8 is equal to the design discharge within a reasonable tolerance.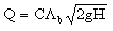
EquationObject271325
Equation 9-8.
where:
  • C
     = discharge coefficient (0.8 typical)
  • H
     = difference between energy grade at cross section 3 and water surface at cross section 2 (ft. or m), Equation 9-9.
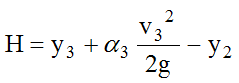
EquationObject272326
Equation 9-9.
where:
  • α
    3
     = kinetic energy correction coefficient
  • C
    d
    = coefficient of discharge, Equation 9-12.
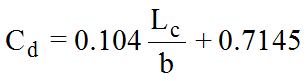
EquationObject273327
Equation 9-10.
where:
  • b
     = width of top of embankment at bridge abutment (ft. or m) (see Figure 9-15)
  • L
    c
    = length of bridge opening between abutment faces (ft. or m).
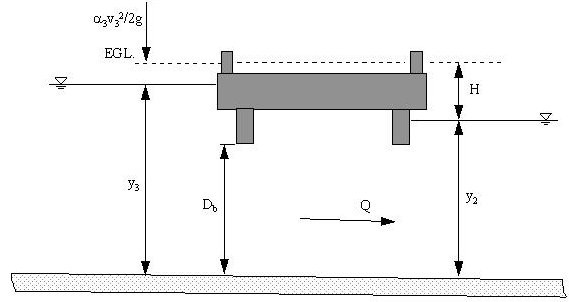    Orifice Type Pressure Flow (click in image to see full-size image)
    Figure 9-14. Orifice Type Pressure Flow
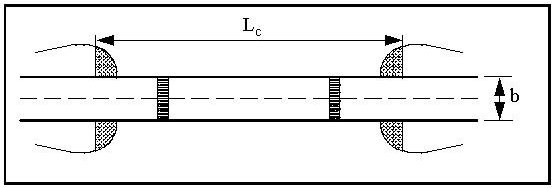    Bridge Dimensions for Pressure Flow Analysis (click in image to see full-size image)
    Figure 9-15. Bridge Dimensions for Pressure Flow Analysis