Momentum Balance Method

This method computes the backwater through Zone 2 by balancing forces at three locations:
  • between the inside, downstream face of the bridge (B
    d
    ) and cross section 2
  • between the downstream and upstream ends of the bridge (B
    d
     to B
    u
    )
  • between the inside, upstream face of the bridge (B
    u
    ) and cross section 3.
Refer to Figure 9-10 and Figure 9-12 for zone and cross section locations. Assuming hydrostatic pressure conditions, the forces acting on a control volume between two cross sections (1 and 2) must be in balance and are generalized in Equation 9-2.
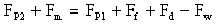
EquationObject265311
Equation 9-2.
where:
  • F
    P1
    ,
    F
    P2
    = force due to hydrostatic pressure at cross section 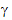InlineEquation50315= Ay
  • F
    m
    = force causing change in momentum between cross sections = ρ Q
    △
     v
  • F
    f
    = force due to friction = 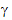InlineEquation50315(A
    1
    +A
    2
    )LS
    f
    /2
  • F
    d
    = total drag force due to obstructions (e.g., for piers = ρ C
    d
    A
    o
    v/2)
  • F
    w
    = component of weight in direction of flow = 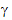InlineEquation50315(A
    1
    +A
    2
    )LS
    o
    /2.
  1. For subcritical flow, determine the water surface elevation and average velocity at section 2 from step backwater computations.
  2. Determine the water surface elevation and average velocity at Section B
    d
     by applying successive assumed water surface elevations to Equation 9-3 until equality is achieved within a reasonable tolerance.
  3. Determine the momentum correction factor (B), which accommodates natural velocity distributions similar to the energy correction factor, α , using Equation 9-4.
  4. Using the resulting water surface elevation at B
    d
    , determine the water surface elevation and average velocity at Section B
    u
     by applying successive assumed water surface elevations at Section B
    u
     to Equation 9-5 until achieving equality within a reasonable tolerance. B
    u
     refers to the upstream face of the bridge.
  5. Determine the final momentum balance between the upstream face of the bridge and cross section 3 using Equation 9-6. Table 9-3 “
    Suggested Drag Coefficients for Bridge Piers
    ” presents suggested drag coefficients for different pier types.
  6. As discussed in the above
    Flow Zones and Energy Losses
    section, proceed with the remainder of the bridge impact computations from cross section 3 upstream using step backwater calculations.
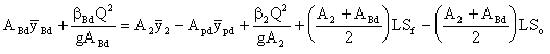
EquationObject266319
Equation 9-3.
where:
  • Subscripts 2 and Bd refer to section 2 and the downstream bridge face, respectively.
  • A
     = effective flow area at cross sections (sq.ft. or m
    2
    )
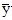  • InlineEquation54320 = height from water surface to centroid of effective flow area (ft. or m)
  • g
     = acceleration due to gravity (ft./s
    2
     or m/s
    2
    )
  • Q
     = discharge (cfs or m
    3
    /s)
  • A
    pd
    = obstructed area of pier at downstream side (sq. ft. or m
    2
    )
  • L
     = distance between cross sections (ft. or m)
  • S
    f
    = friction slope (ft./ft. or m/m) (see Chapter 6)
  • S
    o
    = channel bed slope (ft./ft. or m/m)
  • β = momentum correction factor.
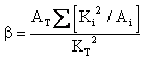  • EquationObject267321
    Equation 9-4.
where:
  • K
    i
    = conveyance in subsection (cfs or m
    3
    /s)
  • A
    i
    = area of subsection (sq. ft. or m
    2
    )
  • K
    T
    = total conveyance of effective area section (cfs or m
    3
    /s)
  • A
    T
    = total effective area (sq.ft. or m
    2
    ).
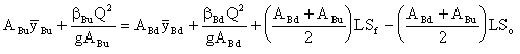
EquationObject268322
Equation 9-5.
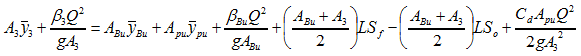
EquationObject269323
Equation 9-6.
where:
  • Subscript 3 refers to cross section 3
  • A
    pu
    = Obstructed area of piers at upstream side (sq.ft. or m
    2
    )
  • C
    d
    = drag coefficient
Table 9-3: Suggested Drag Coefficients for Bridge Piers
Pier Type
Drag Coefficient, C
d
Circular
1.20
Elongated with semi-circular ends
1.33
Elliptical (2:1 aspect ratio)
0.60
Elliptical (4:1 aspect ratio)
0.32
Elliptical (8:1 aspect ratio)
0.29
Square nose
2.00
Triangular nose (30
o
 apex)
1.00
Triangular nose (60
o
apex)
1.39
Triangular nose (90
o
apex)
1.60
Triangular nose (120
o
 apex)
1.72