Energy Equations

Assuming channel slopes of less than 10 percent, the total energy head can be shown as Equation 6-6.
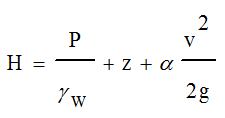
EquationObject200220
Equation 6-6.
where:
  • H
     = total energy head (ft. or m)
  • P
     = pressure (lb./sq.ft. or N/m
    2
    )
  • γ
    w
    = unit weight of water (62.4 lb./cu.ft. or 9810 N/m
    3
    )
  • z
     = elevation head (ft. or m)
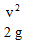    InlineEquation21221 = average velocity head, h
    v
     (ft. or m)
  • g
     = gravitational acceleration (32.2 ft./ s
    2
     or 9.81 m/s
    2
    )
  • α = kinetic energy coefficient, as described in
    Kinetic Energy Coefficient Computation
    section
  • v
     = mean velocity (fps or m/s).
In open channel computations, it is often useful to define the total energy head as the sum of the specific energy head and the elevation of the channel bottom with respect to some datum.
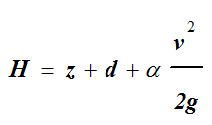
EquationObject201222
Equation 6-7.
where:
  • d
     = depth of flow (ft. or m).
For some applications, it may be more practical to compute the total energy head as a sum of the water surface elevation (relative to mean sea level) and velocity head.
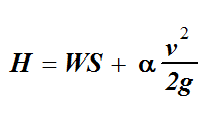
EquationObject202223
Equation 6-8.
where:
  • WS
     = water-surface elevation or stage (ft. or m) = z + d.
Specific Energy Equation.
 If the channel is not too steep (slope less than 10 percent) and the streamlines are nearly straight and parallel, the specific energy, E, becomes the sum of the depth of flow and velocity head.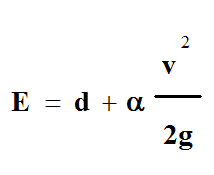
EquationObject203224
Equation 6-9.
Kinetic Energy Coefficient.
 Some of the numerous factors that cause variations in velocity from point to point in a cross section are channel roughness, non-uniformities in channel geometry, bends, and upstream obstructions.
The velocity head based on average velocity does not give a true measure of the kinetic energy of the flow because the velocity distribution in a river varies from a maximum in the main channel to essentially zero along the banks. Get a weighted average value of the kinetic energy by multiplying average velocity head by the kinetic energy coefficient (α). The kinetic energy coefficient is taken to have a value of 1.0 for turbulent flow in prismatic channels (channels of constant cross section, roughness, and slope) but may be significantly different than 1.0 in natural channels. Compute the kinetic energy coefficient with Equation 6‑10:
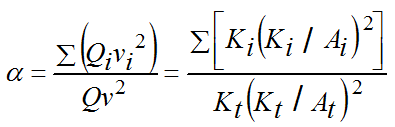
EquationObject204225
Equation 6-10.
where:
  • v
    i
    = average velocity in subsection (ft./s or m/s) (see
    Continuity Equation
    section)
  • Q
    i
    = discharge in same subsection (cfs or m
    3
    /s) (see
    Continuity Equation
    section)
  • Q
     = total discharge in channel (cfs or m
    3
    /s)
  • v
     = average velocity in river at section or Q/A (ft./s or m/s)
  • K
    i
    = conveyance in subsection (cfs or m
    3
    /s) (see
    Conveyance
    section)
  • A
    i
    = flow area of same subsection (sq. ft. or m
    2
    )
  • K
    t
    = total conveyance for cross-section (cfs or m
    3
    /s)
  • A
    t
    = total flow area of cross-section (sq. ft. or m
    2
    ).
In manual computations, it is possible to account for dead water or ineffective flows in parts of a cross section by assigning values of zero or negative numbers for the subsection conveyances. The kinetic energy coefficient will, therefore, be properly computed. In computer models, however, it is not easy to assign zero or negative values because of the implicit understanding that conveyance and discharge are similarly distributed across a cross section. This understanding is particularly important at bends, embankments, and expansions, and at cross sections downstream from natural and manmade constrictions. The subdivisions should isolate any places where ineffective or upstream flow is suspected. Then, by omitting the subsections or assigning very large roughness coefficients to them, a more realistic kinetic energy coefficient is computed.
In some cases, your calculations may show kinetic energy coefficients in excess of 20, with no satisfactory explanations for the enormous magnitude of the coefficient. If adjacent cross sections have comparable values or if the changes are not sudden between cross sections, such values can be accepted. If the change is sudden, however, make some attempt to attain uniformity, such as using more cross sections to achieve gradual change, or by re-subdividing the cross section.