Continuity and Velocity

The continuity equation is the statement of conservation of mass in fluid mechanics. For the special case of steady flow of an incompressible fluid, it assumes the following form:
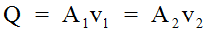
EquationObject195215
Equation 6-1.
where:
  • Q
     = discharge (cfs or m
    3
    /s)
  • A
     = flow cross-sectional area (sq. ft. or m
    2
    )
  • v
     = mean cross-sectional velocity (fps or m/s, perpendicular to the flow area).
  • The superscripts
    1
     and
    2
     refer to successive cross sections along the flow path.
As indicated by the Continuity Equation, the average velocity in a channel cross-section, (v) is the total discharge divided by the cross-sectional area of flow perpendicular to the cross-section. It is only a general indicator and does not reflect the horizontal and vertical variation in velocity.
Velocity varies horizontally and vertically across a section. Velocities near the ground approach zero. Highest velocities typically occur some depth below the water surface near the station where the deepest flow exists. For one-dimensional analysis techniques such as the
Slope Conveyance Method
and
(Standard) Step Backwater Method
(see Chapter 7), ignore the vertical distribution, and estimate the horizontal velocity distribution by subdividing the channel cross section and computing average velocities for each subsection. The resulting velocities represent a velocity distribution.