Channel Capacity

Most of the departmental channel analysis procedures use the Manning’s Equation for uniform flow (Equation 6‑2) as a basis for analysis:
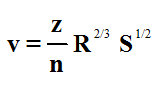
EquationObject196216
Equation 6-2.
where:
  • v
    = Velocity in cfs or m
    3
    /sec
  • z
    = 1.486 for English measurement units, and 1.0 for metric
  • n
     = Manning’s roughness coefficient (a coefficient for quantifying the roughness characteristics of the channel)
  • R
     = hydraulic radius (ft. or m) = A / WP
  • WP
     = wetted perimeter of flow (the length of the channel boundary in direct contact with the water) (ft. or m)
  • S
     = slope of the energy gradeline (ft./ft. or m/m) (For uniform, steady flow, S = channel slope, ft./ft. or m/m).
Combine Manning’s Equation with the continuity equation to determine the channel uniform flow capacity as shown in Equation 6‑3.
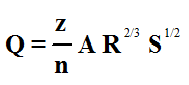
EquationObject197217
Equation 6-3.
where:
For convenience, Manning’s Equation in this manual assumes the form of Equation 6‑3. Since Manning’s Equation does not allow a direct solution to water depth (given discharge, longitudinal slope, roughness characteristics, and channel dimensions), an indirect solution to channel flow is necessary. This is accomplished by developing a stage-discharge relationship for flow in the stream.
All conventional procedures for developing the stage-discharge relationship include certain basic parameters as follows:
  • Q
     = discharge (cfs or m
    3
    /s)
  • z
    = 1.486 for English measurement units, and 1.0 for metric
  • A
     = cross-sectional area of flow (sq. ft. or m
    2
    ).
You need careful consideration to make an appropriate selection and estimation of these parameters.