Accommodation of Outliers

The distribution of all the annual and historical peak discharges determines the shape of the flow-frequency curve and thus the design-peak discharges. The shape of the frequency curve generated by a log-Pearson type III analysis is symmetrical about the center of the curve. Therefore, the distribution of the higher peak discharges affects the shape of the curve, as does the distribution of the lower peak discharges.
Flooding is erratic in Texas, so a series of observed floods may include annual peak discharge rates that do not seem to belong to the population of the series. The values may be extremely large or extremely small with respect to the rest of the series of observations. Such values may be outliers that should be excluded from the set of data to be analyzed or treated as historical data.
Bulletin #17C
calls for identification of these outliers.
Design flows are typically infrequent large flows. Therefore, it is desirable to base the frequency curve on the distribution of the larger peaks. This is accomplished by eliminating from the analyses peak discharges lower than a low-outlier threshold. The value for the low-outlier threshold, therefore, should exclude those peaks not indicative of the distribution for the higher peaks. This value is chosen by reviewing the sequentially ranked values for all peak discharges used in the analysis.
Equation 4-8 provides a means of identifying the low outlier threshold (Asquith et. al 1995):
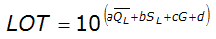
Equation 4-8.
Where:
  • LOT
     = estimated low-outlier threshold (cfs)
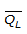  • InlineEquation715 = mean of the logarithms of the annual peak discharge (see Equation 4-3)
  • S
    L
    = standard deviation of the logarithms of the annual peak discharge (see Equation 4-4)
  • G
     = coefficient of skew of log values (station skew, see Equation 4-5)
  • a
     = 1.09
  • b
     = -0.584
  • c
     = 0.140
  • d
     = -0.799
This equation was developed for English units only and does not currently have a metric equivalent.
High outlier thresholds permit identification of extremely high peak discharges with probability smaller than indicated by the period of record for a station. For example, if a true 1% percent chance exceedance (100-year) peak discharge were gauged during a 10-year period of record, the frequency curve computed from the 10 years of record would be unduly shaped by the 1% percent chance exceedance peak.
The
USGS
has made efforts to identify high outliers, referred to as historical peaks, by identifying and interviewing residents living proximate to the gauging stations. In many cases, residents have identified a particular flood peak as being the highest since a previous higher peak. These peaks are identified as the highest since a specific date.
In other cases, residents have identified a specific peak as the highest since they have lived proximate to the gauging station. Those peaks are identified as the highest since at least a specific date. The historical peaks may precede or be within the period of gauged record for the station.
Equation 4-9 provides a means of identifying the high outlier threshold (Bulletin #17B):
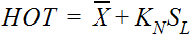
Equation 4-9.
Where:
  • HOT
     = estimated high-outlier threshold (logarithm of flow)
  • N
     = number of systematic peaks remaining in sample after previously detected outliers have been removed
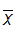  • InlineEquation817 = mean of the logarithms of the systematic annual peak discharges, with previously detected outliers removed
  • S
    L
     = standard of deviation of the logarithms of the annual peak discharges
  • K
    N
     = frequency factor for sample size N from Appendix 4 of Bulletin #17B
All known historical peak discharges and their associated gauge heights and dates appear on the
USGS Texas Water Science
web site.
To incorporate high outlier information when fitting the LPIII distribution according to
Bulletin #17B
procedures, the designer will:
  • Use Equation 4-9 to define the high-outlier threshold.
  • Collect supporting information about the identified high outlying flows.
  • Retain as part of the systematic record any high outlying flows found not to be the maximum flow of record.
  • Extend the period of record for the analysis to include the flow if the flow’s value is found to be the maximum flow of record and lies outside the systematic record. If the value does lie within the systematic record, the period of record is not extended. In both cases, the designer shall recompute the LPIII parameters following the procedure described in Section V.A.9 and Appendix 6 of Bulletin #17B.
  • Thoroughly document data, interviews, decisions, and assumptions used to justify the identification of high outliers and recomputation of LPIII parameters.
TxDOT recommends the use of hydrologic statistical analysis computer programs that can detect outlying values and recomputed LPIII parameters consistent with
Bulletin #17C
 procedures.