The Kerby Method
For small watersheds where overland flow is an important component of overall travel time, the Kerby method can be used. The Kerby equation is
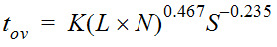
Equation 4-14.
Where:
- t= overland flow time of concentration, in minutesov
- K= a units conversion coefficient, in which K = 0.828 for traditional units and K = 1.44 for SI units
- L= the overland-flow length, in feet or meters as dictated by K
- N= a dimensionless retardance coefficient
- S= the dimensionless slope of terrain conveying the overland flow
In the development of the Kerby equation, the length of overland flow was as much as 1,200 feet (366 meters). Hence, this length is considered an upper limit and shorter values in practice generally are expected. The dimensionless retardance coefficient used is similar in concept to the well-known
; however, for a given type of surface, the retardance coefficient for overland flow will be considerably larger than for open-channel flow. Typical values for the retardance coefficient are listed in Table 4-5. Roussel et al. 2005 recommends that the user should not interpolate the retardance coefficients in Table 4-5. If it is determined that a low slope condition or a transitional slope condition exists, the user should consider using an adjusted slope in calculating the time of concentration. See Time of Concentration.
Generalized terrain description | Dimensionless retardance coefficient (N) |
|---|---|
Pavement | 0.02 |
Smooth, bare, packed soil | 0.10 |
Poor grass, cultivated row crops, or moderately rough packed surfaces | 0.20 |
Pasture, average grass | 0.40 |
Deciduous forest | 0.60 |
Dense grass, coniferous forest, or deciduous forest with deep litter | 0.80 |