Procedure for Using Omega EM Regression Equations for Natural Basins

Equations have been developed for natural basins in 1-degree latitude and longitude quadrangles in Texas. Figure 4-5 shows the geographic extents of each quadrangle. The approach used to develop the regional equations is referred to as the “Regression Equations for Estimation of Annual Peak-Streamflow Frequency for Undeveloped Watersheds in Texas Using an L-moment-Based, PRESS-Minimized, Residual-Adjusted Approach.” (USGS 2009) For development and use of regression equations a natural basin is defined as having less than 10 percent impervious cover, less than 10 percent of its drainage area controlled by reservoirs, and no other human-related factors affecting streamflow (USGS 2001). The equations are therefore not applicable to urban watersheds.
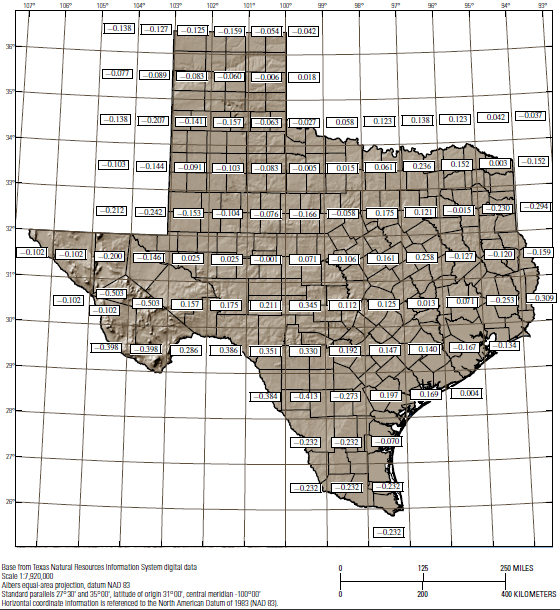
OmegaEM () quadrangles for Texas regression equations. Toview a .pdf of this image, click here. (click in image to see full-size image)
Figure 4-5. OmegaEM (
Ω
)quadrangles for Texas regression equations. To view a .pdf of this image, click
here
.
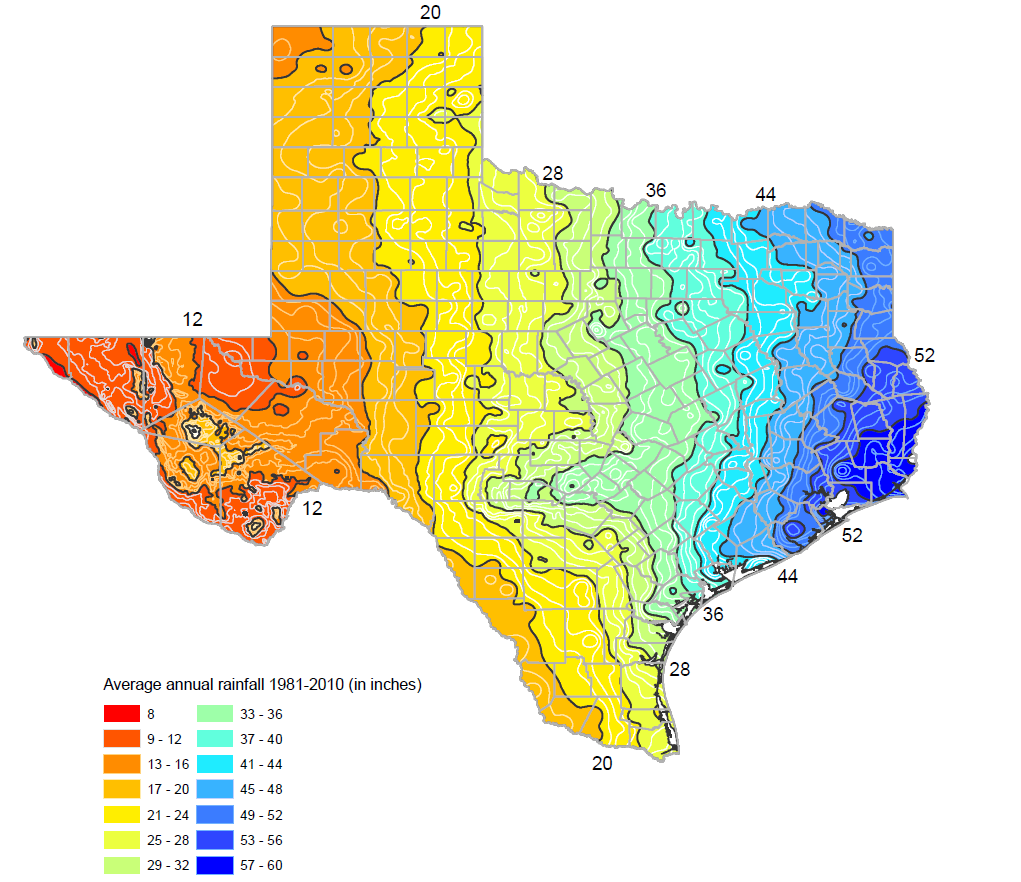
Mean annual precipitation, in inches (Source:Texas Water Development Board 2017) (click in image to see full-size image)
Figure 4-6. Mean annual precipitation, in inches (Source: Texas Water Development Board 2017)
Equation 4-12 is the general form of the Omega EM regression equation for Texas:
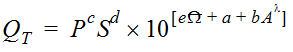
Equation 4-12.
Where:
  • Q
    T
     = peak discharge of recurrence interval
    T
     years (cfs)
  • P = mean annual precipitation in inches from Figure 4-6
  • S = dimensionless main channel slope
  • Ω
     = OmegaEM from Figure 4-5
  • A = contributing drainage area (mi
    2
    )
  • l = a power determined by iterative PRESS-minimization for the recurrence interval
  • a, b, c, d, e
     = regression coefficients specific for the recurrence interval
Mean annual precipitation is the arithmetic mean of a suitably long period of time of total annual precipitation in inches. The mean annual precipitation was assigned based on the approximate center of the watersheds. Asquith and Roussel (2009 TxDOT 0-5521-1) considers that any general and authoritative source of mean annual precipitation for any suitably long period (perhaps 30 years) is sufficient for substitution into the regression equations.
Main channel length is defined as the length in stream-course miles of the longest defined channel from the approximate watershed headwaters to the outlet. Main channel slope is defined as the change in elevation, in feet, between the two end points of the main channel divided by the main channel length in feet.
OmegaEM (
Ω
) parameter represents a generalized terrain and climate index that expresses relative differences in peak-streamflow potential not represented in the watershed characteristics of drainage area, slope, and mean annual precipitation.
Since the gauges used to develop the equations are points in space, and that the variables used (contributing area, slope, precipitation) are actually attributes of that specific point, the OmegaEM should also pertain to the point in question. As such, if the contributing drainage area overlaps more than one quadrant on Figure 4-5, the OmegaEM must not be weighted or averaged. The OmegaEM specific for the quadrant of the site must be selected.
The summary of weighted-least-squares, PRESS-minimized, regional regression equations using drainage area, dimensionless main-channel slope, mean annual precipitation, and OmegaEM are provided in Table 4-4.
RSE, residual standard error in log
10-
 units of cubic feet per second; Adj., adjusted; AIC, Akaike Information Criterion; PRESS, Prediction Error Sum of Squares.
Table 4-4: Regression Equations
Regression Equations
RSE
Adj. R-squared
AIC statistic
PRESS statistic
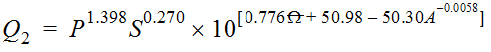0.29
0.84
273
64.6
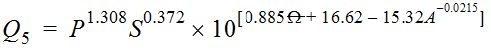0.26
0.88
122
49.1
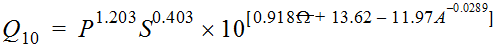0.25
0.89
86.5
46.6
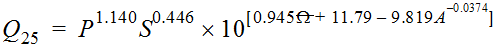0.26
0.89
140
49.5
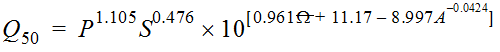0.28
0.87
220
55.6
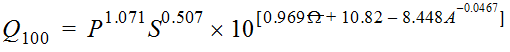0.30
0.86
320
64.8
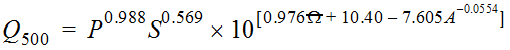0.37
0.81
591
98.7