Gutter Flow

The ponded width is a geometric function of the depth of the water (y) in the curb and gutter section. The spread is usually referred to as ponded width (T), as shown in Figure 10-10.
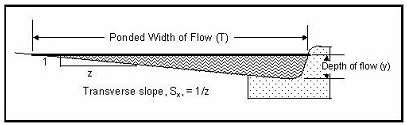
Gutter Flow Cross Section Definition of Terms (click in image to see full-size image)
Figure 10-13. Gutter Flow Cross Section Definition of Terms
Using Manning's Equation for
Depth of Flow
as a basis, the depth of flow in a curb and gutter section with a longitudinal slope (S) is taken as the uniform (normal) depth of flow. (See Chapter 6 for more information.) For Equation 10-1, the portion of wetted perimeter represented by the vertical (or near-vertical) face of the curb is ignored. This justifiable expedient does not appreciably alter the resulting estimate of depth of flow in the curb and gutter section.
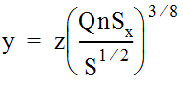
EquationObject278332
Equation 10-1.
where:
  • y
    = depth of water in the curb and gutter cross section (ft. or m)
  • Q
    = gutter flow rate (cfs or m3/s)
  • n
    = Manning’s roughness coefficient
  • S
    = longitudinal slope (ft./ft. or m/m)
  • S
    x
    = pavement cross slope = 1/x (ft./ft. or m/m)
  • z
    = 1.24 for English measurements or 1.443 for metric.
The table below presents suggested Manning's “n” values for various pavement surfaces. Department recommendation for design is the use of the rough texture values.
Table 10-1 Manning’s n-Values for Street and Pavement Gutters
Type of gutter or pavement
n
asphalt pavement:
Smooth texture
Rough texture
0.013
0.016
Concrete gutter with asphalt pavement:
Smooth texture
Rough texture
0.013
0.015
Concrete pavement:
Float finish
Broom finish
0.014
0.016
Refer to Figure 10-10, and translate the depth of flow to a ponded width on the basis of similar triangles using Equation 10-2. Equation 10-2 can also be used to determine the ponded width in a sag configuration, where “y” is the depth of standing water or head on the inlet.
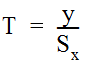
EquationObject279333
Equation 10-2.
where:
  • T
     = ponded width (ft. or m).
Equations 10-1 and 10-2 are combined to compute the gutter capacity.
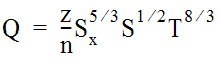
EquationObject280334
Equation 10-3.
where:
  • z
     = 0.56 for English measurements or 0.377 for metric.
Rearranging Equation 10-3 gives a solution for the ponded width, “T”.
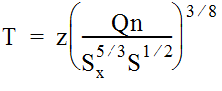
EquationObject281335
Equation 10-4.
where:
  • z
     = 1.24 for English measurements or 1.443 for metric.
Equations 10-3 and 10-4 apply to roadway sections having constant cross slope and a vertical curb. The FHWA publication “
Urban Drainage Design Manual
" (
HEC-22
) should be consulted for parabolic and other shape roadway sections.